Radar: Point Charges, Electric Flux, and Electrostatic Flux
Radar: Point Charges, Electric Flux, and Electrostatic Flux
People say lots of things—usually clichés—and one of those things is that opposites attract. We aren't sure how accurate that is about people, but it's totally true for point charges.
A point charge is a math concept that places an electric charge in a specific location in space, whether that point's positive or negative. A point charge can either have a positive or negative state, with positive charges moving towards negative charges. This is an idea that makes math easier to do, so the decisions on how things work are sometimes arbitrary. (Source)
This idea might seem odd, but it helps understand things like electric flux and electrostatic force. Just like an apple helps describe how gravity works, point charges help explain how electric forces work.
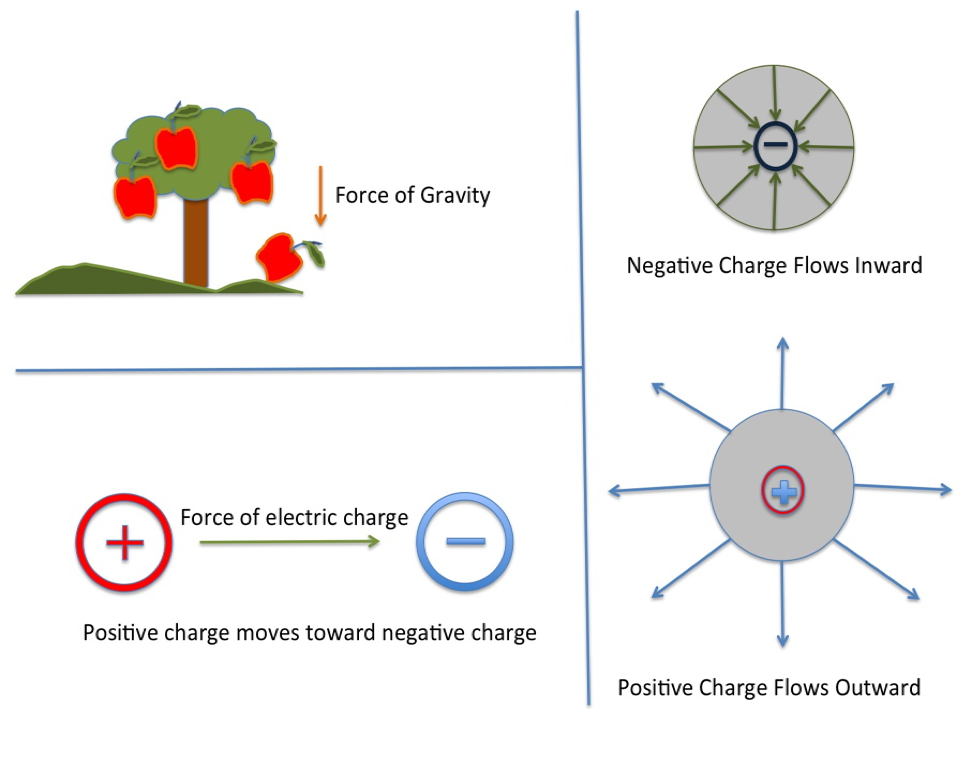
The force between point charges is actually pretty similar to the force of Gravity in Newton's Laws. Say you have two stationary point charges, q and u, separated by a distance, r. Now say that q and u have an associated force, called the electrostatic force, that will either attract or repel the two point charges.
The two point charges will repel—push each other apart—if they both have the same type of charge and will attract—pull together—if their charges are the opposite.
Electric Flux
As for electric flux, imagine a shower, and you've got the general idea of what's going on, except that shower's spraying electric fields—a field of space with some amount of point charges—instead of warm water. That field's moving at a specific rate of flow. Who doesn't love a nice warm spray of point charges early in the morning? (Source)
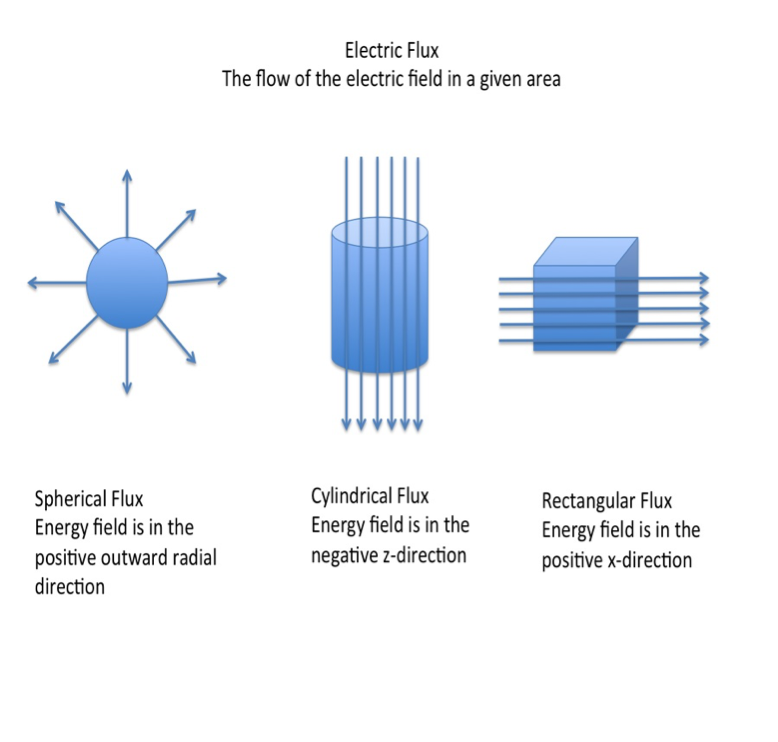
An electric flux generally moves through an area that is perpendicular to the electric field. Sounds simple, right?
Too simple. If we have uniform electric field, E, passing through a surface, with surface area S, then the equation for electric flux, φ, is just
φ = EScos(θ)
where θ is the angle of the wave as it travels through the field. If you ever, heaven forbid, have a non-uniform field with a complex surface area, everything gets way more complex. We won't get into all the dirty deets, but just know that you could take courses on this stuff without necessarily mastering it.
(Source)