We're going to be doing a lot of problems making fish sticks or pizza slices or linguine pasta out of different foods. Since mathematicians are lazy, and because we should be focused more on our knife skills–we like our fingers–we're going to make some assumptions to save time and space later.
From now on, assume that
- all vertical slices have width Δ x and all horizontal slices have thickness Δ y. That way we don't have to keep saying "take a vertical slice of a guava with width Δ x."
- when we say "the height of the slice is ..." we mean "the approximate height of the slice is ...". Similarly when we say "the area of the slice is ..." we mean "the approximate area of the slice is ..." That way we don't have to keep saying the word "approximately." As much as we like that word, we're going to sound like a Star Wars drone if we keep saying it.
- once we know the area of a slice, we can write down the integral that gives the area of the whole region. We don't have to write "we add up all the approximate regions and take the limit as the number of slices goes to ∞ to get an integral" every single time.
- if a problem asks us to "write an integral expression" for the area of a region, that means we don't need to evaluate the integral. If you want to practice evaluating integrals, then by all means, feel free to do them. We're focusing on how to set up the integrals in this chapter, which is the most difficult part for most people. We can save ourselves the headache of solving them for another day.
Example 1
Let R be the region bounded by the graph of y = x2 and the line y = 4. Write an integral expression for the area of R, using (a) vertical slices (b) horizontal slices |
Example 2
Let R be the region between the graphs |
Exercise 1
Let R be the region above the line  and below the graph of y = cos x on the interval
and below the graph of y = cos x on the interval 
Write an integral expression for the area of R,
(a) vertical slices
(b) horizontal slices
Exercise 2
Let R be the region bounded by the curve y = x4 and the lines x = 2 and y = 81. Write an integral expression for the area of R, using
(a) vertical slices
(b) horizontal slices
Exercise 3
Let R be the region in the first quadrant bounded by the graph of x2 + y2 = 1 and the x- and y- axes. Write an integral expression for the area of R, using
(a) vertical slices
(b) horizontal slices
Exercise 4
Let R be the region bounded by the graphs of y = ex, y = 1, and x = 3.
Write an integral expression for the area of R, using
(a) vertical slices
(b) horizontal slices
Exercise 5
Let R be the region above the graph of y = 1 – x2 and below the graph x2 + y2 = 1. Write an integral expression for the area of R, using vertical slices.
Exercise 6
Let R be the region in the first quadrant bounded by the x-axis and the graphs  and y = 5 – x2. Write an integral expression for the area of R, using horizontal slices.
and y = 5 – x2. Write an integral expression for the area of R, using horizontal slices.
Exercise 7
Let R be the region in the first quadrant bounded by the line y = 5 and the graphs  and y = 5 – x2. Write an integral expression for the area of R, using horizontal slices.
and y = 5 – x2. Write an integral expression for the area of R, using horizontal slices.
Exercise 8
Let R be the region between the graphs  , y = x2, and the line x = 4.
, y = x2, and the line x = 4.
Write an integral expression for the area of R, using vertical slices.
Exercise 9
Let R be the region in the first quadrant bounded by the x-axis and the graphs  and y = 5 – x2. Write an integral expression for the area of R, using vertical slices.
and y = 5 – x2. Write an integral expression for the area of R, using vertical slices.
Exercise 10
Let R be the region in the first quadrant bounded by the line y = 5 and the graphs  and y = 5 – x2. Write an integral expression for the area of R, using vertical slices.
and y = 5 – x2. Write an integral expression for the area of R, using vertical slices.
Exercise 11
Let R be the region between the graphs of y = x4 + 1 and y = x2 + 1 for 1 ≤ y ≤ 5. Write an integral expression for the area of R, using
(a) vertical slices
(b) horizontal slices
Exercise 12
Let R be the region shown below.

Write an integral expression for the area of R, using vertical slices.



 . There's another option that's even easier. Since the region R consists of two identical pieces, we can integrate from 0 to 2 and multiply the result by 2. Another expression for the area of R is
. There's another option that's even easier. Since the region R consists of two identical pieces, we can integrate from 0 to 2 and multiply the result by 2. Another expression for the area of R is  . This area is simple to integrate, but we won't do it here.
. This area is simple to integrate, but we won't do it here.
 . The width of the slice is twice the x-coordinate, or
. The width of the slice is twice the x-coordinate, or  :
: . The slice at the bottom of R is at "height" y = 0, and the slice at the top is at "height" y = 4. So the limits of integration are from 0 to 4, and the area of R is
. The slice at the bottom of R is at "height" y = 0, and the slice at the top is at "height" y = 4. So the limits of integration are from 0 to 4, and the area of R is  . This area is more difficult to integrate than the vertical slices. We could do it here, but we should be glad we don't have to. We dodged a bullet.
. This area is more difficult to integrate than the vertical slices. We could do it here, but we should be glad we don't have to. We dodged a bullet. , y = x2, and the line x = 4. Write an integral expression for the area of R using horizontal slices.
, y = x2, and the line x = 4. Write an integral expression for the area of R using horizontal slices.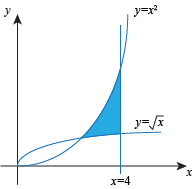
 .
. , and one piece where the horizontal slices go from the graph y = x2 to the line x = 4. Let's look at the lower piece first, and start by figuring out the limits of integration.
, and one piece where the horizontal slices go from the graph y = x2 to the line x = 4. Let's look at the lower piece first, and start by figuring out the limits of integration. to a point on the graph of
to a point on the graph of  with coordinates
with coordinates , so its area is
, so its area is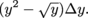
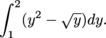
 , so the area is
, so the area is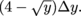
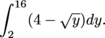
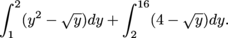
 :
:
 . This is the region R:
. This is the region R: on this interval, the height of the slice at position x is
on this interval, the height of the slice at position x is

 . The integral expression
. The integral expression


 to y = 1.
to y = 1.










 . Since y also ranges from 0 to 1, the area of R is
. Since y also ranges from 0 to 1, the area of R is













 (or x = 2y) on the left to the graph of y = 5 – x2 (or
(or x = 2y) on the left to the graph of y = 5 – x2 (or  ) on the right:
) on the right: , and the area of the slice is
, and the area of the slice is


 on the right.
on the right. , so the area of that slice is
, so the area of that slice is

 :
:


 , the line x = 2, and the x-axis. The piece on the right is bounded by the graph y = 5 – x2, the line x = 2, and the x-axis. Let's look at the piece on the left first. The slice at position x has height
, the line x = 2, and the x-axis. The piece on the right is bounded by the graph y = 5 – x2, the line x = 2, and the x-axis. Let's look at the piece on the left first. The slice at position x has height  , and x runs from 0 to 2. The area of the piece on the left is
, and x runs from 0 to 2. The area of the piece on the left is
 (since this is where the graph of 5 – x2 crosses the x-axis).
(since this is where the graph of 5 – x2 crosses the x-axis).

 .
.
 .
.

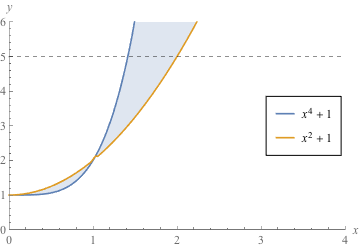
 . The graph y = x2 + 1 intersects the line y = 5 when x = 2.
. The graph y = x2 + 1 intersects the line y = 5 when x = 2. the graph of y = x4 + 1 is on top.
the graph of y = x4 + 1 is on top. the graph of y = 5 is on top.
the graph of y = 5 is on top.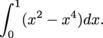
 .
.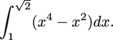
 .
.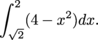
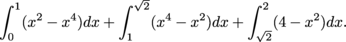
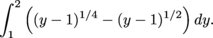
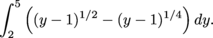
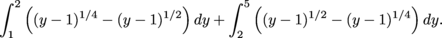
 immediately:
immediately:
 from
from  :
: ,
, .
. , because, for
, because, for  , the upper bound of R is a line, and for
, the upper bound of R is a line, and for  , the upper bound of R is the circle.
, the upper bound of R is the circle. the upper bound of R is a line that goes through the origin and has slope
the upper bound of R is a line that goes through the origin and has slope
 .
. ) is
) is

 in the left piece of R, the area of the left piece of R is
in the left piece of R, the area of the left piece of R is .
. the upper bound of R is the equation of the circle, x2 + y2 = 1 or
the upper bound of R is the equation of the circle, x2 + y2 = 1 or .
. ) is
) is

 to
to  in the right piece of R, the area of the right piece of R is
in the right piece of R, the area of the right piece of R is
