Some things to remember for implicit differentiation:

- Since y is a function of x, any derivative involving y must use the chain rule.
- Since y is a function of x, taking the derivative of xy (or of any other product involving both x and y) requires the product rule.
- Since y is a function of x, taking the derivative of
 (or any other quotient involving both x and y) requires the quotient rule.
(or any other quotient involving both x and y) requires the quotient rule.
With these things in mind, we're ready to get cracking.
Example 1
Find x2 + y2 = 4. |
Example 2
What is the derivative of y with respect to x given that 4y2 + 8y = 2x2? |
Example 3
Assuming y is a function of x and xy + x = y, what is |
Exercise 1
Use implicit differentiation to find  , assuming that y is a function of x.
, assuming that y is a function of x.
- 4y = x
Exercise 2
In the following equation what is the derivative of y with respect to x?
- sin y = x2
Exercise 3
Find the derivative of y with respect to x in the following equation
- ln (xy) = x + y
Exercise 4
Find  in the following equation.
in the following equation.
- y3 + x2y – x = y
Exercise 5
What is  in the following equation?
in the following equation?
 given that
given that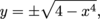
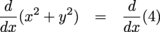
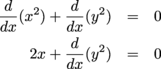
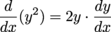
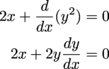
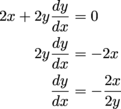
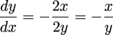


 , but that's fine. We can factor them out:
, but that's fine. We can factor them out:

 ?
?

 , so we can rewrite the equation as
, so we can rewrite the equation as

 and
and  , so we find
, so we find
 , so move all the terms with that on one side and factor:
, so move all the terms with that on one side and factor:








 terms on one side and solve:
terms on one side and solve:

 .
.
 terms on one side, factor, and solve:
terms on one side, factor, and solve:



 to one side, factor, and solve:
to one side, factor, and solve: