It's good to have a feel for what continuity at a point looks like in pictures. However, sometimes we're asked about the continuity of a function for which we're given a formula, instead of a picture. When this happens, remember that the following three statements must all hold for f to be continuous at c.
- I. The function f is defined at x = c.
- The limit
 exists.
exists.
- The value f(c) agrees with the limit

Example 1
Determine whether the function is continuous at x = 1. |
Example 2
Determine whether the function
is continuous at x = 2. |
Example 3
Determine whether the function
is continuous at x = 0. |
Example 4
Determine whether the function
is continuous at x = 0. |
Example 5
At what values is f discontinuous?
|
Exercise 1
Determine whether the function

Exercise 2
For what values of x is the function discontinuous.
Exercise 3
For the function, determine all values at which the function is discontinuous.
Exercise 4
For what values of x is h(x) discontinuous.

 to see if it exists. As x approaches 1 from the left, we find
to see if it exists. As x approaches 1 from the left, we find 


 , f is continuous at x = 1.
, f is continuous at x = 1.





 does not exist, and the function is not continuous at x = 0.
does not exist, and the function is not continuous at x = 0.
 doesn't exist since
doesn't exist since  .
.
 does not exist, or where
does not exist, or where  . Think of such values as problem spots. We need to look at the function's definition and find these "problem spots".
. Think of such values as problem spots. We need to look at the function's definition and find these "problem spots".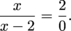
 when x < 0. Since 2 > 1, we have f(2) = 4.
when x < 0. Since 2 > 1, we have f(2) = 4. . When
. When  we're using the piece of the function definition that says
we're using the piece of the function definition that says
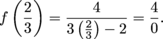
 .
. not exist?
not exist? , which we've already taken care of.
, which we've already taken care of.
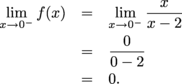
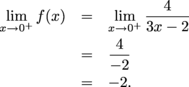
 does not exist, and f is discontinuous at x = 0.
does not exist, and f is discontinuous at x = 0. exist?
exist?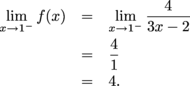
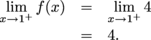
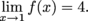
 disagree. Again, we only need to inspect those values of c where the function's definition changes over. Since
disagree. Again, we only need to inspect those values of c where the function's definition changes over. Since  the function f is continuous at 1.
the function f is continuous at 1. and x = 0.
and x = 0.
 exists and agrees with f(-4). As x approaches -4 from the left, we use the part of the function definition that says
exists and agrees with f(-4). As x approaches -4 from the left, we use the part of the function definition that says  The left-sided limit is
The left-sided limit is 


 the function is continuous at x = 0.
the function is continuous at x = 0.
 .
.  is undefined. Therefore
is undefined. Therefore does not exist, and f is discontinuous at x = 2.
does not exist, and f is discontinuous at x = 2. which is undefined. Therefore f is discontinuous at x = 3.
which is undefined. Therefore f is discontinuous at x = 3.




 is undefined,
is undefined,  is also undefined and g is discontinuous when x = 1. That's the only troublesome spot we need to check.
is also undefined and g is discontinuous when x = 1. That's the only troublesome spot we need to check.




