Way back when we started learning trig, it was all about the triangles. Since then, we've branched out to waves and circles and formulas—and, aside from our special triangles, we pretty much lost sight of triangles. Don't you miss them?
Now they are back and ready for action. We get to do triangle trig again, only this time it's about more than just side length ratios. Let's use trig to find the area of a triangle.
We all know the basic formula for the area of a triangle is 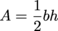 , where b = any base of the triangle and h = the height of the triangle from that base. What happens if we don't know the height of the triangle? You guessed it, panic and tears. It will be hours before we calm down. Or, instead, we can use trig.
, where b = any base of the triangle and h = the height of the triangle from that base. What happens if we don't know the height of the triangle? You guessed it, panic and tears. It will be hours before we calm down. Or, instead, we can use trig.
Here's a triangle to help us see what we're doing:
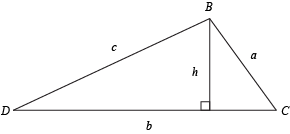
We can see that h is a part of a right triangle with angle C and side a. They all get together Thursday nights to hang out and play a game of Risk. Looking at the triangle, we can tell that:
sin C = h⁄a
Solving this for h gets us:
h = b sin C
A little sleight of hand will slip this into our formula, allowing us to perform the neat trick of finding the area without needing the height.
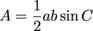
Let's go ahead and give it a try.
Sample Problem
Find the area of this triangle:
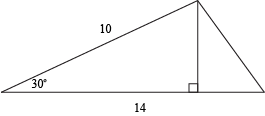
We have a new formula,  . We have a = 14 units, b = 10 units, and C = 30°. We also have a dog, a plan, and a canal. Once we get a pagoda, we'll have the whole set.
. We have a = 14 units, b = 10 units, and C = 30°. We also have a dog, a plan, and a canal. Once we get a pagoda, we'll have the whole set.

We could cram 35 units2 worth of stuff inside this triangle. That's almost enough space to fit our collection of Hot Wheels.
This formula will work for any triangle, as long as we know an angle and its two adjacent sides. The two sides have to be right next to the angle. That's our one restriction. We don't need to spend time stressing over which side to put where in the formula.
Sample Problem
What is the area of a triangle with an angle of 60° and two adjacent sides measuring 5 cm and 7 cm?
We don't need a picture or anything here; we could do it blindfolded, even. We have two sides and an angle so we know we can use our area formula.

Not the prettiest answer ever, but at least it's exact. And correct, that's a good one too. If we're really bothered by it, we can ask the nearest calculator to tell us that this equals 15.2 cm2.