If the equation of a line is in slope-intercept form, it looks like this:
y = mx + b
Here's what those extra letters mean:
- m is the slope of the line.
- b is the y-intercept.
Let's look at a few examples:
The equation y = 2x + 1 is in slope-intercept form. The coefficient of the x-term is 2, so the slope is 2. The constant is 1, so the y-intercept is 1. That means the graph passes through the point (0, 1).
In the equation y = 4 – 8x, the slope is -8 (the coefficient of the x-term) and the y-intercept is 4. Don't let the order of the terms trip you up: we can rearrange it so it looks like y = -8x + 4.
In the equation y = -9x, the slope is -9 and the y-intercept is 0, since there's no constant.
Remember: the slope (m) is equal to the change in y divided by the change in x, or "rise over run."
Slope-intercept form of a line: y = mx + b
Let's examine how to graph an equation in slope-intercept form. What does the graph of y = 2x + 1 look like?
Our equation is in slope-intercept form, so we know that the number in front of x is the slope (2), and 1 is the y-intercept.
We start by plotting the y-intercept.

Next, since we know that the slope is 2, also known as  , we know that another point will be 2 units up and 1 unit over (in the positive direction of course).
, we know that another point will be 2 units up and 1 unit over (in the positive direction of course).

Finally, we connect these points.

What if the equation isn't solved for y already? Well, we'll just have to solve it for y, won't we ?
Graph 2x + 3y = 18.
First things first: solve for y by subtracting the 2x term and dividing by 3.
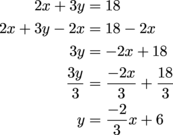
Now our equation is in slope-intercept form and we can graph it.
We put a point at 6 on the y-axis since 6 is the y-intercept. From there, we "rise" -2, which means we go down 2 units, but we don't put a point there yet. We still need to "run" 3 to the right. Then we put the point down.

Look Out: when using slope-intercept form to graph lines, always make sure the equation is solved for y so that the equation is in the form y = mx + b.