ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Angles Videos
Play All
Unlike anything that enters the Bermuda Triangle, Exterior angles can be found—in more than one way. This video covers how to use the remote inte...
Not to be confused with complimentary angles, which are just the nicest angles you'll ever meet.
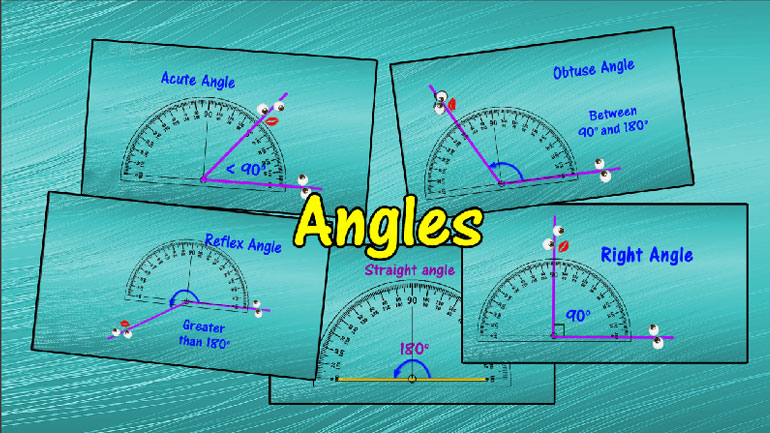
So what's our angle? We want to help you learn about angles. Really—that's it. Shmoop has distilled our angle knowledge into a short video that w...
This video explains similar figures and how to figure out if two shapes are similar using sides and angles. Plus, it discusses how to use one shape...
This video explains similar figures and how to figure out if two shapes are similar using sides and angles. Plus, it discusses how to use one shape...