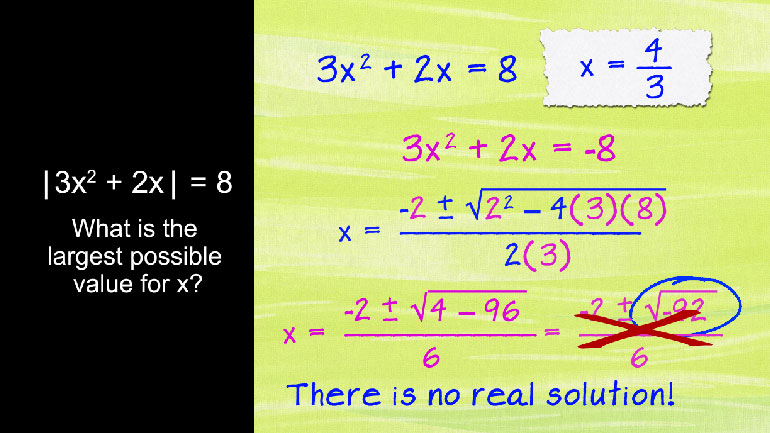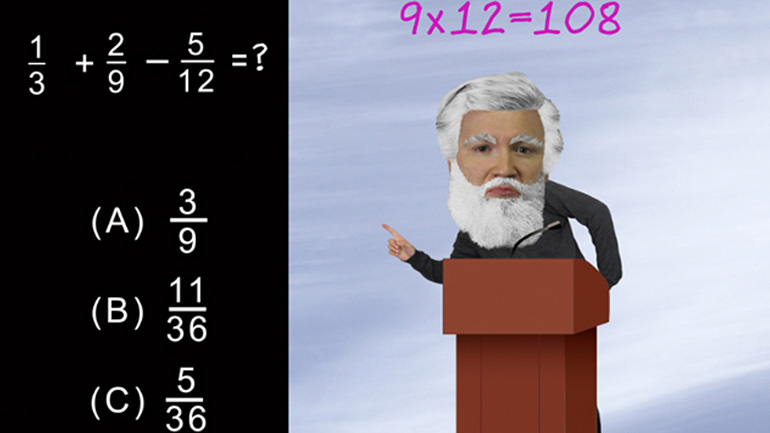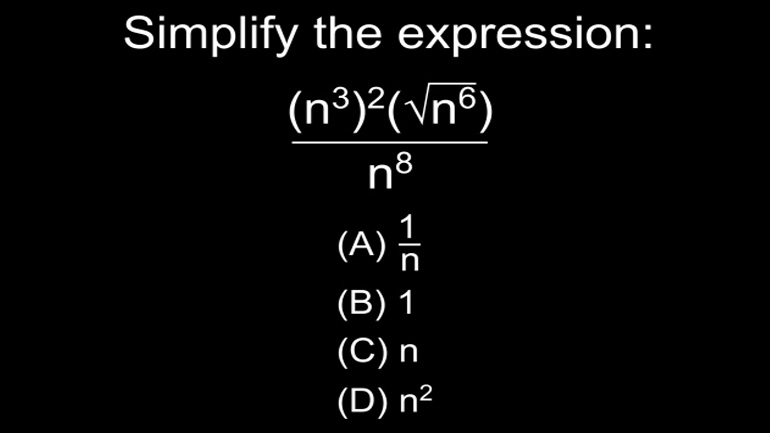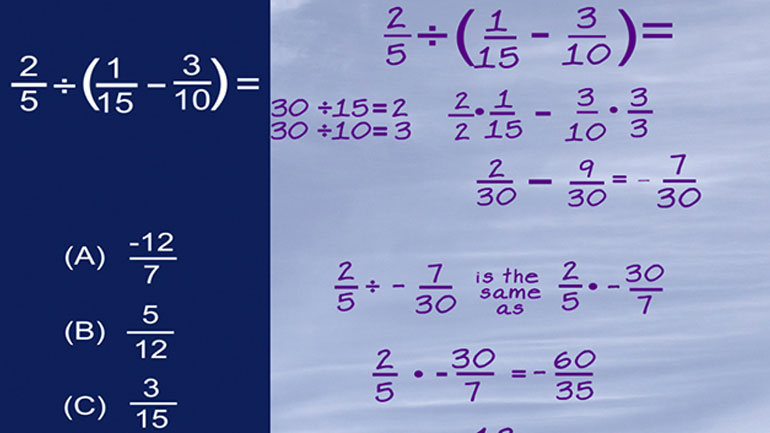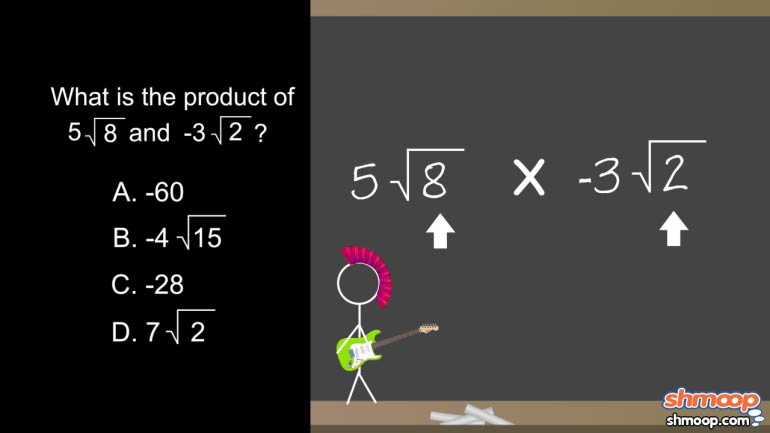ShmoopTube

Check out this video to learn more about absolute value and how it has no patience for negative signs.

We love doing absolute value problems because it means spending time with our good buddy, the number line. But don’t think we’ve forgotten abou...

The easy way to remember the look of an absolute value graph is that they are always a V-shape... and “V” stands for value. Or for verisimilitu...

Solving two-step equations can be tricky, but at least they’re easier than doing the Texas Two-Step. We trip over our feet so often you’d think...

SAT Math 3.6 Numbers and Operations

Sometimes, we just want fewer y's...or more x's. That's why it's great to know how to add and subtract variables. In real life, though, we try to a...

ACT Math Elementary Algebra Drill 4, Problem 2. Solve for x.

ACT Math: Pre-Algebra Drill 2, Problem 1. Solve for x in this equation.

ACT Math Pre-Algebra: Drill 2, Problem 2. Solve for y.

This video covers Least Common Multiple and Greatest Common Factor. What are they? How do you find them? How does factorization play in?

Number Sense: Drill Set 5, Problem 1. Solve the equation.

We just had a brilliant idea for a new Transformer: Optimus Prime Factorization.

This video helps you tackle two-step equations with multiplication and division by using the opposite operation on each side of the equation. Defin...

Leftovers are good. Remainders are not.

Just because some numbers are only a single digit, doesn't mean they don't still deserve a little love.

CAHSEE Math Algebra and Functions: Drill Set 1, Problem 4. Which operation should be performed first?

Algebra and Functions: Drill Set 3, Problem 2. Simplify the expression in this video.

Algebra and Functions Drill 3 Problem 4. Simplify the expression.

Those itty-bitty exponents are difficult to read as it is. Now they're going to be even smaller—and include fractions? Someone had better get us...

SAT Math 1.4 Numbers and Operations. Solve the equation.

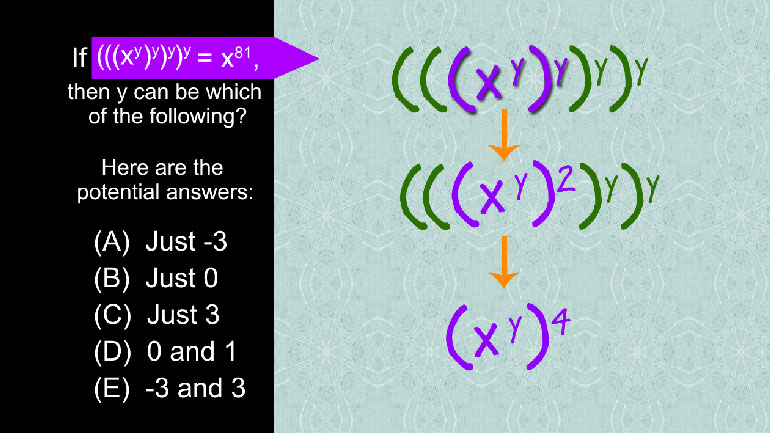
SAT Math 2.2 Algebra and Functions. What value of y is correct?

SAT Math 3.2 Numbers and Operations

SAT Math 1.4 Algebra and Functions. Solve for x.

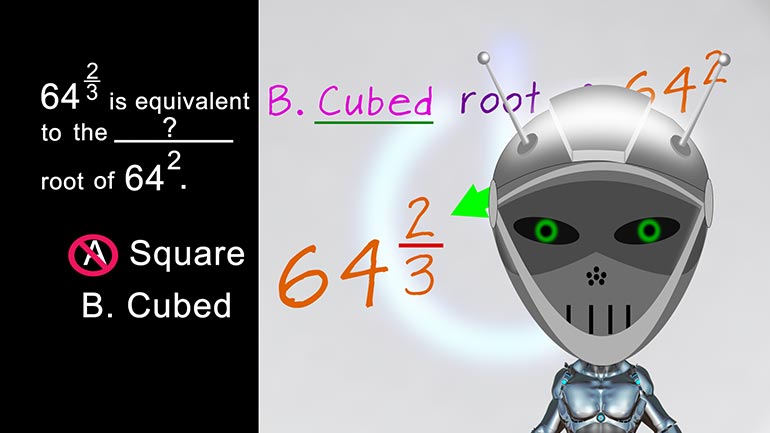
GED Math 1.3 Rational Numbers. Which answer best fills in the blank?

CAHSEE Number Sense: Drill Set 1, Problem 1. How would he write the number in scientific notation?

CAHSEE Math Number Sense: Drill Set 1, Problem 2. The decimal 0.000035 can be written in scientific notation as...what?

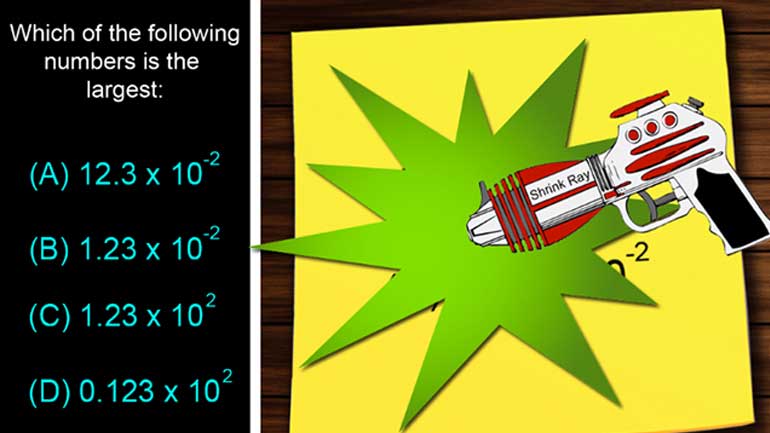
CAHSEE Math Number Sense: Drill Set 1, Problem 3. Which of the following numbers is the largest?