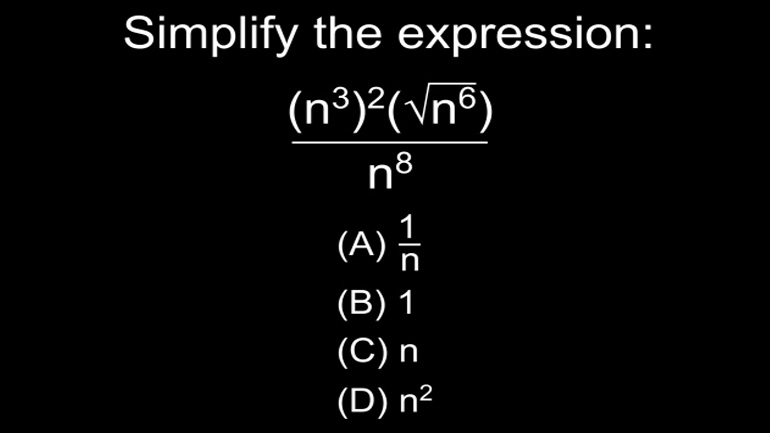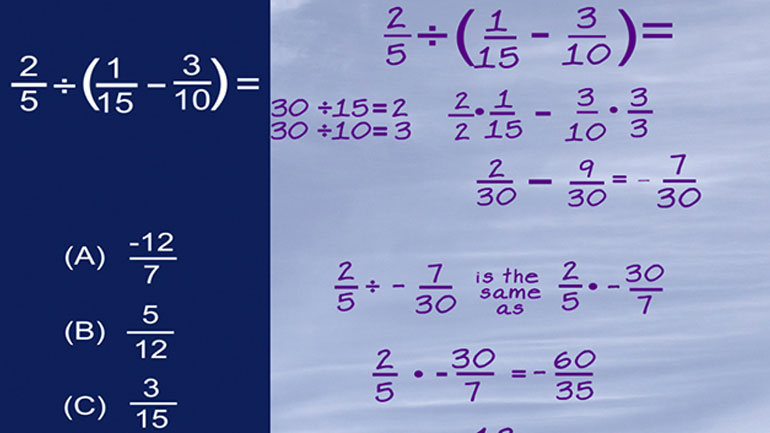ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Order of Operations (PEMDAS) Videos
Play All
CAHSEE Math 1.4 Algebra and Functions
299 Views
CAHSEE Math Algebra and Functions: Drill Set 1, Problem 4. Which operation should be performed first?
CAHSEE Math 3.2 Algebra and Functions
201 Views
Algebra and Functions: Drill Set 3, Problem 2. Simplify the expression in this video.
CAHSEE Math 3.4 Algebra and Functions
235 Views
Algebra and Functions Drill 3 Problem 4. Simplify the expression.
Introduction to PEMDAS
6614 Views
Please Excuse My Dear Aunt Sally. What did she do? Slander the process of order of operations?