ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Powers and Exponents Videos
Play All
SAT Math 1.4 Numbers and Operations. Solve the equation.
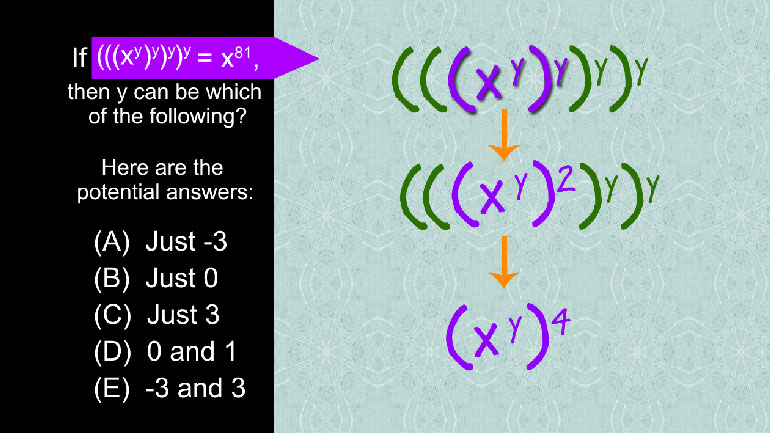
SAT Math 2.2 Algebra and Functions. What value of y is correct?
Numbers have friends in high places: they're called powers. And yes, they are powerful. They can make a single digit number turn into a 10 digit nu...
Exponents desperately want to be like regular ol' numbers—so it figures they also want to be multiplied and divided.
Those itty-bitty exponents are difficult to read as it is. Now they're going to be even smaller—and include fractions? Someone had better get us...