ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Scientific Notation Videos
Play All
CAHSEE Math 1.1 Number Sense
753 Views
CAHSEE Number Sense: Drill Set 1, Problem 1. How would he write the number in scientific notation?
CAHSEE Math 1.2 Number Sense
394 Views
CAHSEE Math Number Sense: Drill Set 1, Problem 2. The decimal 0.000035 can be written in scientific notation as...what?
CAHSEE Math 1.3 Number Sense
460 Views
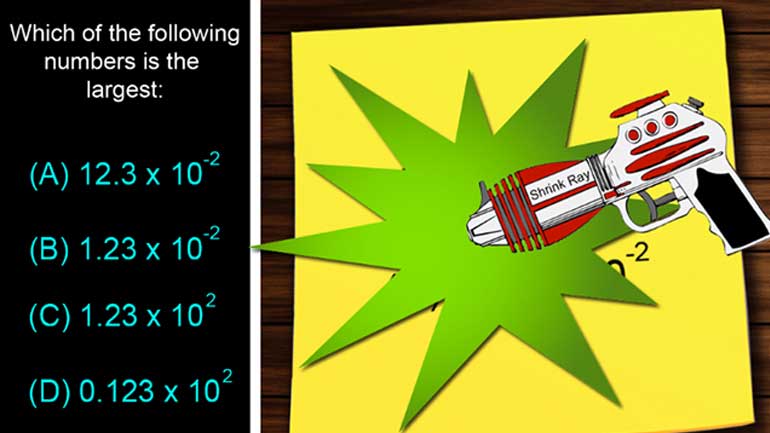
CAHSEE Math Number Sense: Drill Set 1, Problem 3. Which of the following numbers is the largest?
Scientific Notation
25564 Views
Ever wish you didn't have to write out all those zeros when you counted your mounds of money? Well, there's a solution for that: scientific notatio...