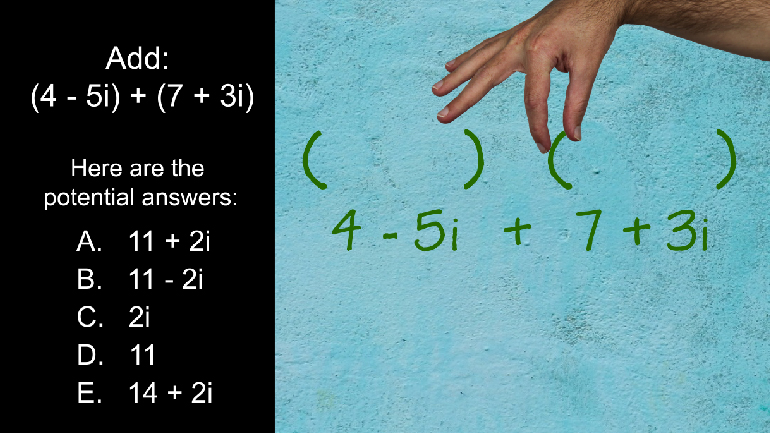ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Use complex numbers in polynomial identities and equations Videos
Play All
ACT Math 2.2 Elementary Algebra
253 Views
Elementary Algebra Drill 2: Problem 2. Can you find the product?
ACT Math 4.4 Intermediate Algebra
358 Views
ACT Math: Intermediate Algebra Drill 4, Problem 4. Add these together.
ACT Math 1.2 Intermediate Algebra
700 Views
ACT Math Intermediate Algebra Drill 1, Problem 2. Find the product of (2a + 6)2.