As for the statistics part, you can actually make a living out of doing statistics. In fact, there are even statistics about statisticians.
As for probability, here's a fun yet oddly practical subject, depending on what you do in your spare time. Probabilities are what determine how good your poker hand is. Of course, we know you're only playing for Werther's Originals with your grandmother and not in some seedy, underground club. Even still, knowing probabilities can help you clean out your nana's stash of sweets.
Sample Problem
What's the probability that a five-card poker hand contains four of a kind?
The probability that the hand contains four of a kind is
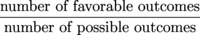 .
.
First, the numerator:
A favorable outcome is any hand that contains four of a kind. Depending on how many Werther's Originals are in the pot, it could be a very favorable outcome indeed. Don't forget...our cut is 20%.
There are 13 different kinds we could get four of (four aces, four 2s, four 3s, and so on.). Once we get four of a kind in our hand, we've already filled 4 of the 5 spaces. There are
52 – 4 = 48
cards left, and we could have any of those. That means there are
13 × 48 = 624
possible hands containing four of a kind.
Next, the denominator:
The number of possible outcomes is the total number of possible five-card poker hands. Since we don't care about the order of the cards, this is a combination question. Given 52 cards, how many ways can we choose five of them? The answer is:

Now we've got the top and bottom of our fraction. The probability of a five-card poker hand containing four of a kind is
 ,
,
which is a pretty tiny number. You wouldn't think so from watching poker scenes in movies, where someone seems to have four of a kind every other hand. Ah, Hollywood. Reflecting real life since 1902.
For more fun with poker, you and your nana should head over here.