We're through with the parallelograms. That's all of the major quadrilaterals, right? Uh...not so much.
There are a couple more families of quadrilaterals that don't really fit inside any nice box. They don't have the nice right angles of squares and rectangles or the equilateral sides of rhombi. They don't even have parallel sides like parallelograms. They're quadrilaterals gone wild. Basically, they've descended into anarchy.
Well, maybe it's not that bad. They aren't crazy, but they certainly don't play by the same rules that squares and parallelograms do. Right angles? They're for suckaz. Parallel sides? Who needs 'em! Kites are free riders, lone wolves who do whatever they want whenever they want. Ish.
A kite is shaped just like what comes to mind when you hear the word "kite." It might not have have a line with colorful bows attached to the flyer on the ground, but it does have that familiar, flying-in-the-wind kind of shape.
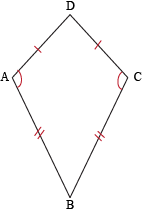
What makes a kite different from the rest of the quadrilateral kingdom? A kite is a type of quadrilateral with two pairs of consecutive congruent sides. Note that we're not in Parallelogram Country anymore, so these consecutive congruent sides don't mean that all sides are congruent. (If they were, we'd be looking at a very specific type of kite: a rhombus.)
If we look at kite ABCD, sides AB and BC are congruent, sharing ∠ABC. Sides CD and DA are congruent and share ∠ADC. What about the other two angles? If you must know (which you must), the angles that connect two non-congruent sides in a kite are congruent. In this case, ∠BAD ≅ ∠DCB.
From looking at ABCD, we see that it's symmetric about one of the diagonals. They don't have to be symmetric about the other diagonal. Because of this special type of property involving the diagonals, each of the diagonals gets its own name. We'll call them the main diagonal and the cross diagonal (but you can call them Sonny and Cher if you want).
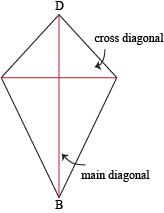
The main diagonal is the larger of the two diagonals (the "Cher" diagonal, obviously). It's the diagonal that's also the kite's line of symmetry. The cross diagonal is the smaller of the two diagonals (the "Sonny" of the two), and it doesn't necessarily involve any symmetry. But these diagonals can do more than sing a killer duet of "I Got You Babe." They've actually got some pretty nifty properties too.
For example, the diagonals of a kite are always perpendicular. So even with their free spirits and lack of order, there's simply no escaping those right angles.
And the patterns don't end there. Since the main diagonal is a line of symmetry, the cross diagonal must be cut in half by the main diagonal. In other words, the main diagonal is perpendicular bisector of the cross diagonal. Of course, that's where geometry and celebrities differ: Cher did not cut Sonny in half, despite whatever any conspiracy theory might claim.
Sample Problem
Prove that the main diagonal of a kite is the perpendicular bisector of the kite's cross diagonal.
Saddle up, because this proof might be a bit of a doozy. Of course, it still gets to the heart of what virtually all quadrilateral proofs are about: finding a lot of congruent triangles.
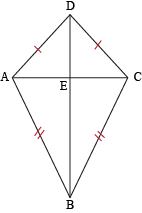
To prove that DB is the perpendicular bisector of AC, we can prove that AE ≅ CE and DB ⊥ AC. Ready? And break!
| Statements | Reasons |
| 1. ABCD is a kite | Given |
| 2. AD ≅ CD and AB ≅ CB | Consecutive sides of a kite are congruent (1) |
| 3. DB ≅ DB | Reflexive Property |
| 4. ΔABD ≅ ΔCBD | SSS Postulate (2, 3) |
| 5. ∠ADB ≅ ∠CDB | CPCTC (4) |
| 6. ΔADC is isosceles | Definition of isosceles triangle (2) |
| 7. ∠DAE ≅ ∠DCE | Isosceles Triangle Theorem (2, 6) |
| 8. ΔAED ≅ ΔCED | ASA Postulate (2, 5, 7) |
| 9. AE ≅ CE | CPCTC (8) |
| 10. ∠DEA ≅ ∠DEC | CPCTC (8) |
| 11. m∠DEA = m∠DEC | Definition of congruent angles (10) |
| 12. m∠DEA + m∠DEC = 180° | Linear pairs are supplementary, definition of supplementary angles |
| 13. 2(m∠DEA) = 180° | Substitution (11, 12) |
| 14. m∠DEA = 90° | Algebra (13) |
| 15. ∠DEA is a right angle | Definition of a right angle (14) |
| 16. DB ⊥ AC | Definition of perpendicular (15) |
| 17. DB is a perpendicular bisector of AC | Definition of perpendicular bisector (9, 16) |
Whew! We've done it, fair and squ—er, kite.
If you hadn't guessed it by now, there's more to the main diagonal than being a perpendicular bisector. It's also a bisector of the internal angles at either end. It only makes sense seeing as how the main diagonal is a line of symmetry and the two triangles are congruent. There were signs everywhere, so hopefully you saw that one coming.
Sample Problem
In kite WXYZ, WY is has length 15 units, and ZX has length 30 units. What is the length of AW?
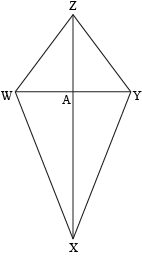
The cross diagonal is WY in this case, because it's shorter than the main diagonal. Since ZX is the main diagonal, it bisects WY into two pieces: AW and AY, each equaling half the length of WY. We know that WY = 15 units, so AW = 15 ÷ 2 = 7.5 units in length.
What if, given the same information, we wanted to find the length of AX? We hate to break it to you, but we can't calculate the length of AX without more information. Yes, the main diagonal bisects the cross diagonal, but the cross diagonal does not usually bisect the main diagonal. So without more information about WXYZ, we can't find the value of AX.
We're sure you're devastated, so just imagine being outside on a beautiful, sunny day. It's hot and humid, and you decide to treat yourself to an ice cream sundae. After paying the vendor, you eat the first few spoonfuls quickly. Too quickly. What happens next? You guessed it: brain freeze.
The pain surges up to deep inside your brain and fear consumes you. Your delicious ice cream is melting in the heat and there's not enough time to wait for the pain to subside. So what do you do? You drop the ice cream and rush to get a glass of water, hoping some hydration will wash away the pain. Luckily, it helps. But once you get back, you see a quadrilateral eating your ice cream. The nerve of some polygons!

You suspect the devious culprit is a kite, but you want to be certain. How are you going to know for sure? Two easy ways:
- If two distinct pairs of consecutive sides of the quadrilateral are congruent, then it's a kite.
- If one of the diagonals bisects the other diagonal at a perpendicular angle, it's a kite.
Sample Problem
You're able to discern that your ice cream thief is a rhombus. Is he also a kite?
Yes, a rhombus is a kite. A rhombus has two distinct sets of congruent sides (all of the sides are congruent), and the diagonals bisect each other at perpendicular angles. Guilty as charged.