The last family of quadrilaterals are the outcasts. They're different from the rest of the quadrilaterals, kind of like the socially awkward guest at the quadrilateral party.

While the rest of them have their congruent sides and angles to chitchat about, these quadrilaterals just hang by the snack bar. Every once in a while, they might strike up a conversation with a lonesome polygon who happens to wander over, but it never lasts long and they just go back to uncomfortably staring at their feet.
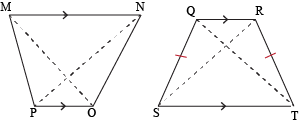
A trapezoid is a quadrilateral with only one set of parallel sides. They absolutely cannot have two sets of parallel sides. So when trapezoids start their own party after being kicked out of the quadrilateral party, we can be certain that rectangles, squares, and parallelograms will definitely not be on the guest list. Take that, suckers.
Sample Problem
Is this quadrilateral a trapezoid?

How many pairs of parallel lines do you see? The top and bottom are parallel to each other, as are the two sides. Since this has two pairs of parallel lines, and a trapezoid must have only one, this is not a trapezoid. Sorry, buddy.
Like kites with their special diagonals, trapezoids also have parts with special names (although none as strange as the names we have for our parts). A trapezoid has two bases, each of which is one of the parallel sides. The other two sides that aren't parallel to each other are called the trapezoid's legs.
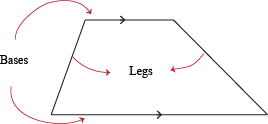
Since only the bases are parallel and the legs are not, we can think of this scenario as two nonparallel transversals cutting across a pair of parallel lines.
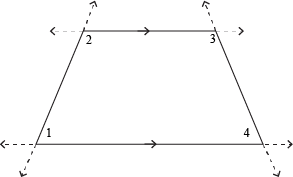
Looking at ∠1 and ∠2, we can see that they are consecutive interior angles. Same goes for ∠3 and ∠4. We already know (thanks to our extensive background in working with parallel lines) that consecutive interior angles are supplementary, so we've proven that consecutive angles in a trapezoid that share the same leg are supplementary.
When both legs of the trapezoid are the same length, we have a special type of quadrilateral called an isosceles trapezoid.
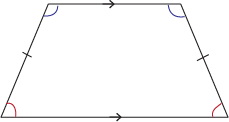
As you might expect, isosceles trapezoids have congruent legs as well as congruent consecutive angles shared by a base. Of course, while isosceles triangles only have one "base" to work with, isosceles trapezoids have two. Double the fun, we say.
Sample Problem
If trapezoid JANE is isosceles and one of its base angles is 73° in measure, what are the measures of the other three angles?
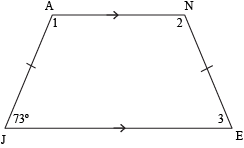
There are many different ways of figuring out the measures of ∠1, ∠2, and ∠3, but we'll start off with the fact that in an isosceles trapezoid, both angles that share a base are congruent. Since the 73° angle and ∠3 share base JE, they're congruent. In other words, m∠3 = 73°.
We also know that since ∠2 and ∠3 are consecutive interior angles, they're supplementary. We know the measure of ∠3, so let's find the measure of ∠2.
m∠2 + m∠3 = 180°
m∠2 + 73° = 180°
m∠2 = 180° – 73°
m∠2 = 107°
What about ∠1? Since it shares a base with ∠2, these two angles are congruent to each other. That means m∠1 = 107° as well.
We can double check this by remembering that all quadrilaterals have interior angles that add up to 360°. If we take the sum of these four angles, that's the number we should get.
73° + 73° + 107° + 107° ≟ 360°
360° = 360°
Yup. Those are the angles we've got. No doubt about it.
Every quadrilateral has its VIPs, or Very Important Polygons. The already exclusive trapezoid club is no exception. The VIPs of the trapezoid family are the isosceles trapezoids. If they aren't glorified for their congruent base angles and legs, then their diagonals do the talking. Yes, that's right: isosceles trapezoids have congruent diagonals. Don't believe us? We'll give you a hint: it's due to a little something called SAS. (No, not "sass.")
Another type of VIP in the trapezoid realm is the right trapezoid, which has one right angle. Of course, wherever that right angle is, it'll have another consecutive to it because the bases are parallel to each other.
Even though not all trapezoids are created equal, we'll need something to unify all trapezoids so they don't have a civil war or something. So we'll give each trapezoid—even those regular old non-isosceles ones—this belt-like thing called a median. It levels the playing field and also helps them suck in those guts after a hearty Thanksgiving meal.
The median of a trapezoid is a segment parallel to the bases that connects the midpoints of the non-parallel sides. This line is special because we can determine its length directly from the length of the two bases. No joke.
The length of the median of a trapezoid, L, is one-half the sum of the lengths of the bases, B1 and B2.

Sample Problem
Quadrilateral ABCD is a trapezoid, and EF is the median of the trapezoid. What is the length of EF?
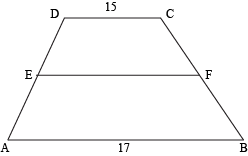
Since we know the lengths of the two bases, we can use the median formula to find this length.
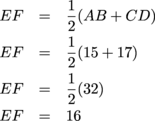
Median EF is 16 units in length.