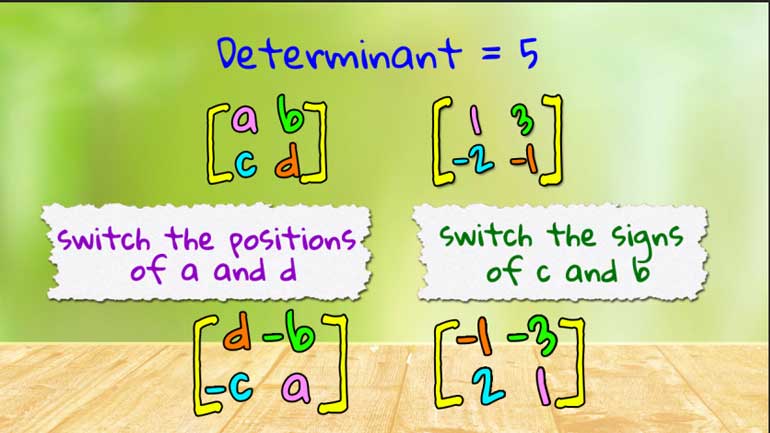
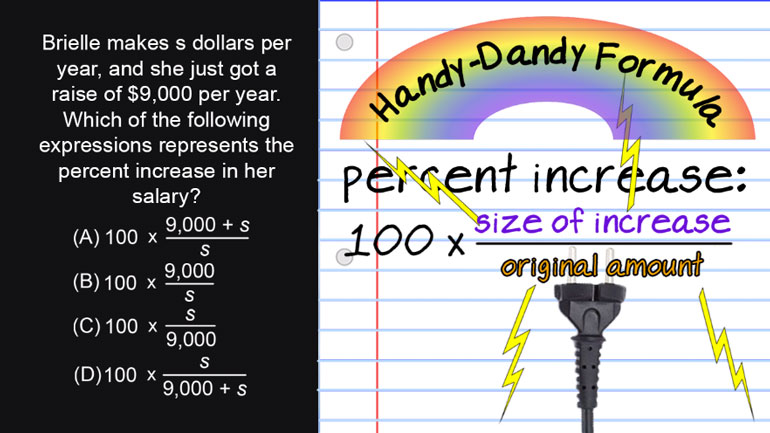
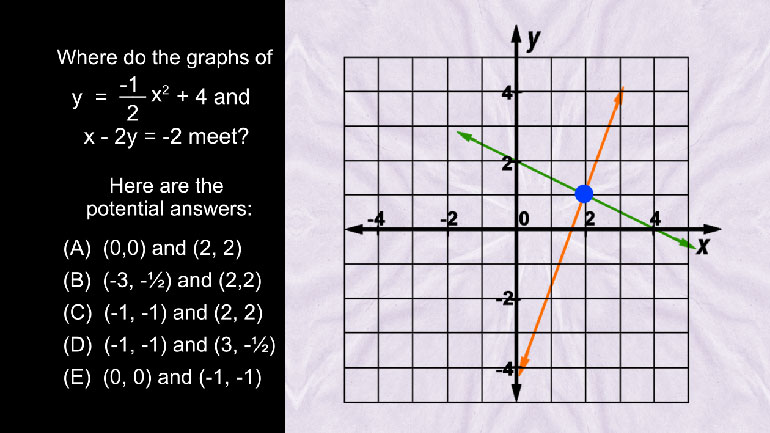
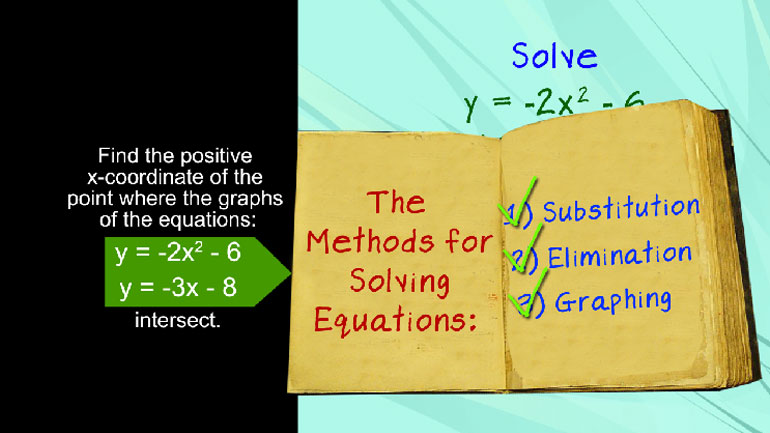
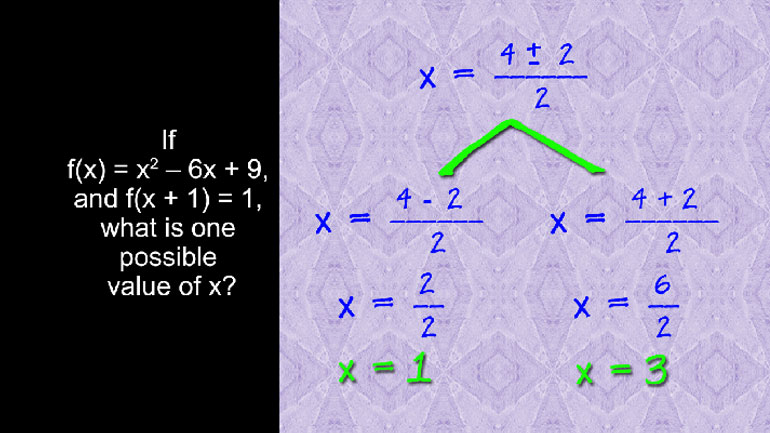
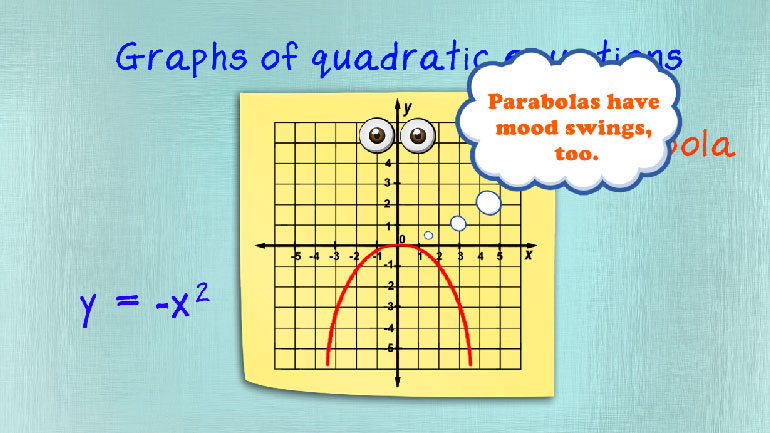
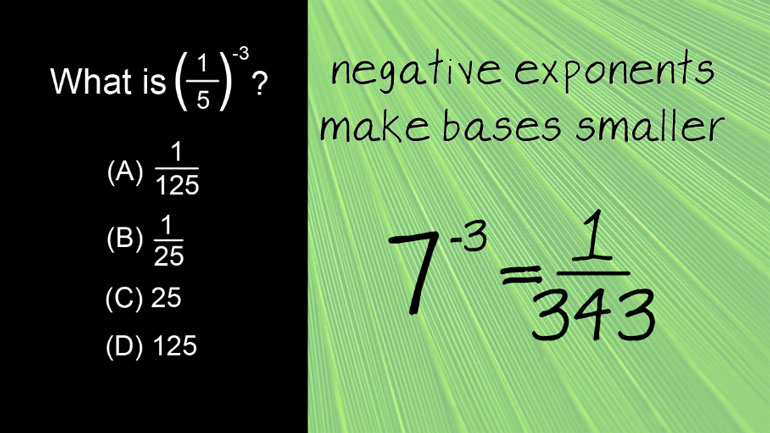ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Algebra II Videos
Mosquitos need their caffeine, just like the rest of us. Wouldn't think zipping around and stinging people all day long sap your energy?
Functions Videos 3 videos
Direct variation helps to calculate exponential proportions and is an easy way to figure out relations. If Godzilla were chasing you, which car wou...
In this video, we meet Slash McFender, a rock 'n' roller with a habit of forgetting his guitar at home. Slash has the brilliant idea to use his ch...
Polynomials and Rational Expressions Videos 17 videos
Rational expressions are too complex... it's about time someone simplified them.
It's impressive that these expressions are able to stay so rational even when they're having operations performed on them.
Multiplying rational expressions is as easy as adding the exponents and simplifying. Ta da!
Sequences and Series Videos 8 videos
Sequences are nice. Without them, there would be no rhyme or reason to anything—no way to ever know what’s coming next. And it would make tryin...
Help Pepe on his quest to once again become the "Pizza King." Or put that healthy metabolism to use and steal his title. Ten slices in less than a...
SAT Math 1.5 Numbers and Operations. How many dots would be in the 5th term of this sequence?