Ratios
One thing most people overlook when planning to move to a new town is figuring out how many dangerous creatures live there. We won't make the same mistake, and luckily we have ratios to help us out.
A ratio is a way of comparing how much we have of two related things¬—say, vampires and werewolves.
Ratios can be written in three different ways. If your town has 25 vampires and 10 werewolves, the ratio of vampires to werewolves can be written as:
25 to 10
25:10

Notice that the last way looks a lot like a fraction. Ratios can even be reduced, exactly as we would reduce a fraction. By dividing both numbers by 5, that same ratio can be written as:
5 to 2
5:2

Proportions
When two ratios are equivalent, they can be written as a proportion. A proportion is two equal ratios. That doesn't always mean they have the same numbers in them. Here's what it does mean:
- If we simplify one ratio and simplify the other, they'll be equal.
- If we rewrite the ratios as decimals, they'll be equal.
- If the number of items in the first ratio goes up, the number of items in the second ratio will go up too.
- If a number is missing in one ratio, we can use the other ratio to figure it out.
Let's say the neighboring town has 5 vampires and 2 werewolves, so the ratio is  . But how does their ratio compare to our town? When we simplify
. But how does their ratio compare to our town? When we simplify 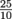 , we get
, we get  , so we know the two towns have the same ratio of vampires to werewolves. We can write these ratios as a proportion.
, so we know the two towns have the same ratio of vampires to werewolves. We can write these ratios as a proportion.
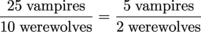
In other words, a ratio of 25 vampires for every 10 werewolves is the same thing as 5 vampires for every 2 werewolves. We'd better rethink moving to this town.
Notice that the number of vampires is in both numerators, and the number of werewolves is in both denominators. Proportions always need to be set up like this, so that the numerators measure the same thing and the denominators measure the same thing. Keeping everyone in their proper place avoids epic battles of mythical creature power.