A proportion is two equal ratios. If we know that two ratios are equal and we only know one of them, we can use it to hunt down the other one.
Proportions, or equal ratios, are super convenient for finding missing measurements. For example, in some preschools the ratio of students to teachers in a classroom must always be 4 students to 1 teacher, or  . If the number of students doubles, then the number of teachers needs to double, too. If there are 8 students, there need to be 2 teachers. If it triples so that there are 12 students, there need to be 3 teachers. If there are 20 students, we can continue to use the original ratio to figure out how many teachers we'd need.
. If the number of students doubles, then the number of teachers needs to double, too. If there are 8 students, there need to be 2 teachers. If it triples so that there are 12 students, there need to be 3 teachers. If there are 20 students, we can continue to use the original ratio to figure out how many teachers we'd need.
Method 1: Multiplication
To find a missing value in a proportion, we multiply both sides of the proportion by the denominators to help solve the equation.
Let's go back to preschool. The ratio of students to teachers is  . If there are 20 students in a classroom, how many teachers will that classroom need?
. If there are 20 students in a classroom, how many teachers will that classroom need?
We first write a set of equal ratios. We know the first ratio is 4 students to 1 teacher. In the second ratio, there are 20 students and an unknown number of teachers, represented by t. Written as fractions, our proportion becomes:
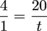
Now the idea is to multiply both sides of our equation by something that'll get rid of those pesky fractions. Remember, we can do anything we want to our equation, as long as we do it to both sides. The denominator of the left side is 1 and the denominator of the right side is t, so we'll multiply both sides by 1t, or just t.
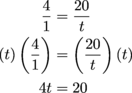
See how those t's on the right side canceled each other out? Nice. Now we solve for t like normal by dividing both sides by 4.
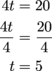
And there's our answer: t = 5. If there are 20 students, there need to be 5 teachers.
Method 2: Equivalent Fractions
After writing our equal ratios, we can sometimes solve for the missing number without using the multiplying trick. Sometimes we can figure out what we need to multiply both the numerator and denominator of the first fraction by to make it equal to the second fraction. If so, it's our lucky day. Let's look at the preschool problem again.
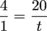
If these ratios are equal, someone's done something to the numerator 4 to change it into the numerator 20. Aha! They multiplied it by 5.

"No fair, foul play," calls the denominator 1, and it isn't fair at all. To keep things fair, we multiply the denominator 1 by 5 as well.

Since 1 times 5 is 5, the missing denominator is t = 5.
The really important part for both methods is to make sure we're comparing apples to apples and oranges to oranges. If we're comparing students to teachers on one side of the equal sign, we must also compare students to teachers on the other side (not teachers to students). The units for both numerators must match, and the units for both denominators must match.
Check out this baffling baking situation:
Your great-grandma's chocolate bourbon-ball cookie recipe calls for 3 cups of flour and 6 tablespoons of brown sugar. Unfortunately, you only have 2 cups of flour, so you can only make a small batch. You need to match the proportion of flour to brown sugar in the recipe (great-grandma wouldn't have it any other way). How much brown sugar do you need?
The recipe calls for a ratio of 3 cups flour to 6 tablespoons brown sugar. That's a ratio of  , which reduces to
, which reduces to 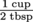 . (It's okay to set up ratios where the measurements are different, like cups and tablespoons.)
. (It's okay to set up ratios where the measurements are different, like cups and tablespoons.)
You only have 2 cups of flour, but the ratio of flour to brown sugar needs to stay constant. The unknown quantity, the amount of brown sugar we need, will be represented with the variable x. So our proportion looks like this:
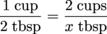
As you can see, the units of the numerators match and the units of the denominators match, with cups of flour on top and tablespoons of brown sugar on the bottom for both. We can drop the units for now, but we'll come back for them later.

Now we can solve for x in one of two different ways:
| Multiplication | Equivalent Fractions |
We've got a denominator of 2 on the left and a denominator of x on the right, so we need to multiply both sides by 2 and by x. In other words, multiply by 2x. The 2s cancel each other out on the left side.  And the x's cancel on the right side.  (Note: if there were a number in front of the variable, we'd divide both sides by that number to get x by itself.) So x = 4. Wait, we're not done. We need to remember the units. We were solving for tablespoons, so we need 4 tablespoons of brown sugar. | In this method we're making equivalent fractions, or ratios. Since we can multiply the numerator of the first ratio by 2 to get the numerator of the second, all we need to do is multiply the denominator of the first ratio by 2 as well. Since 2 × 2 = 4, we need 4 tablespoons of brown sugar. |