ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Sequences and Series Videos
Play All
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
ACT Math: Intermediate Algebra Drill 3, Problem 2. Find the sixth number in the series.
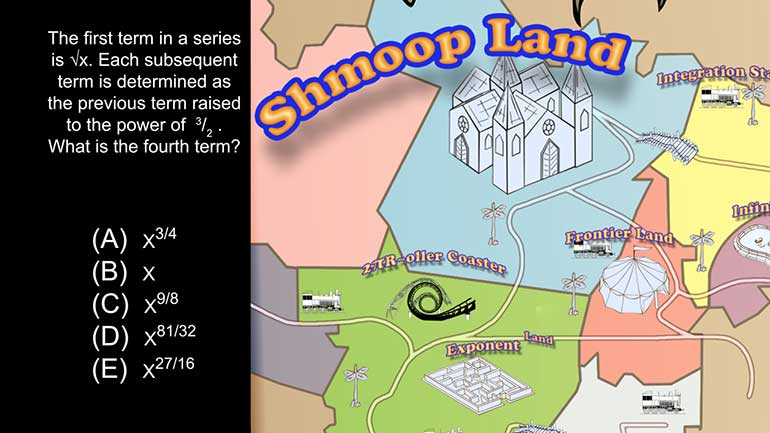
ACT Math: Pre-Algebra Drill 4, Problem 2. What is the fourth term in the series?
SAT Math 1.5 Numbers and Operations. How many dots would be in the 5th term of this sequence?
SAT Math 2.1 Numbers and Operations. How many dots will be in the 6th term of this sequence?
Sequences are nice. Without them, there would be no rhyme or reason to anything; no way to ever know what’s coming next. It would make trying to...