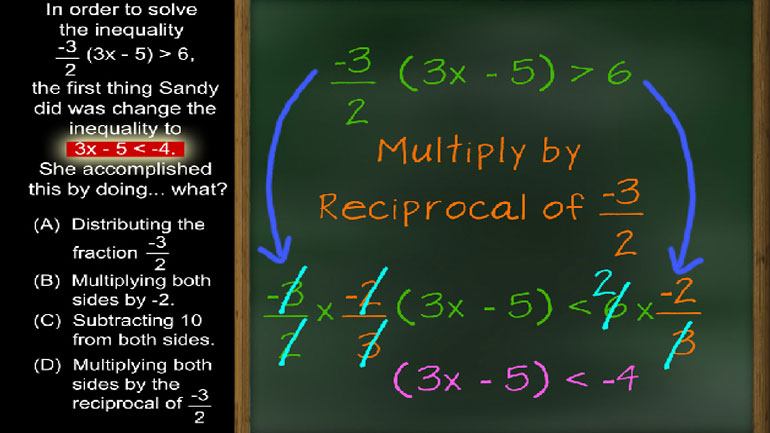ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Linear Inequalities Videos
Play All
When graphing inequalities, you graph the line, shade the corresponding side, and plug in the point. The end!
No, these are not inequalities that have been convicted and imprisoned inside a maximum security prison. Although some of them do have quite a rap...
Algebra I Drill 3 Problem 2. How did Sandy change the inequality?
SAT Math 1.1 Algebra and Functions. Find an algebraic equation to correspond with the data.
Pick the expression that best represents the cost in dollars of riding m miles in a taxi.