The Unit Circle Resources
Best of the Web. Picked by our PhDs
Websites

Well? CAN YOU? (Our bet is on, "Yes.")

There are 15 questions about the sine, cosine, and tangent of different angles. There's no pressure, no time limit, and a happy smiley face when you get it right. Daww.

Just because a function is a little…odd, doesn't mean you can't be friends. Learn a bit about them, and maybe they won't seem so weird. Oh, and some functions are even, or not odd nor even; click the link, and maybe see what's up with that.
Videos

Our pal Patrick sweetly talks us through remembering all the standard angles for the unit circle. We're getting sleepy from his dulcet tone…and more knowledgeable.

Quick—you only have 6 minutes to find the corresponding acute angle of  . Spend 5 minutes watching this video, then use the last minute doing what it tells you to find the angle.
. Spend 5 minutes watching this video, then use the last minute doing what it tells you to find the angle.

In this video, a poor, defenseless trigonometric equation is meticulously and methodically picked apart for your education.

We have a weak spot for good time-lapse videos. Add in a catchy math song, and we are hooked.
Games and Tools

Drag the line around the unit circle to see what that angle is in both degrees and radians. Every time you go a full 360 degrees around, the red spiral grows ever larger. Did you know that 30,000 degrees equals 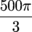 ? We just can't stop spinning it around.
? We just can't stop spinning it around.

There are 16 standard angles on a unit circle. How fast can you identify each one? Beat the high score and win a fabulous not-prize. *Note: not-prize has a value of no-value. Not available in stores.*

A website capable of solving trig equations? We are this freaking close to Skynet, it's frightening.