Kinetic and Potential Energy
While momentum is crucial to our understanding of mechanics, it doesn't tell the whole story. There are whole sets of phenomena that are very hard to describe from an impulse/momentum/force standpoint. Over several centuries a whole bunch of smart scientists got together and developed a mathematical tool for dynamics problems they called energy. The thing that those scientists didn't realize, though, is that energy is way more than a way to keep track of the numbers—it's vital to the way the universe fits together and functions.
Energy, formally defined, is the ability of an object to do mechanical work (we'll dig into this a few sections from now). That means anything with energy has the ability to move other objects, or create light, heat, sound—there's a whole bunch of forms energy can take.
In mechanics, we're concerned with mechanical energy (surprise), which describes the energy associated with an object's motion and position. We say that an object with the ability to move has potential energy (based on its position, it can move, but hasn't yet), while a moving object has kinetic energy; usually an object will have a mixture of both potential and kinetic energy. The other forms energy can take will come into play in later chapters, when we look at electric energy, chemical energy, radiant energy, thermal energy, and more.
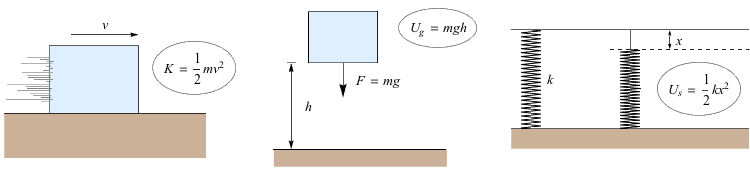
Kinetic energy (K) in mechanics is the product of half an object's mass (m) and its velocity (v) squared:
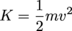
Energy is measured in units of kg⋅m2/s2, which is defined as a joule (J). It scales differently than momentum—the square in the velocity term means faster objects have much more energy than their slower counterparts.
Potential energy (U) is based on an object's position. It can come in different forms. We'll deal primarily with gravitational potential energy and spring potential energy. Gravitational potential energy is given by:
Ug = mgh
Here m is an object's mass, g is the acceleration due to gravity at the earth's surface, and h is an object's height. We can choose to place the h = 0 point anywhere that's convenient for us; gravitational potential energy is a completely relative measurement (and it's fine if it's negative, to boot).
Usually we'll choose h = 0 to be the ground, so that h is actually a height, but sometimes it makes more sense to define h = 0 to be a useful point in our problem—say, the top of a roller coaster. As long as we keep track of negative signs, this is fine.
For example, as Yoda lifts Luke's X-wing out of the Dagobah swamp he is increasing its gravitational potential energy. To determine how much gravitational potential energy Yoda gives to the X-wing, we would need to define h = 0 to be the ground. If we defined it as the surface of the swamp, we would not account for the full height Yoda has lifted it. Thus, knowing the mass and the full height Yoda lifts the X-wing, as well as the gravitational acceleration of Dagobah, determine its gravitational potential energy we can.
Spring potential energy is given by:
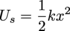
Where k is the spring's coefficient of stiffness and x is its compression distance. The more an object compresses a spring, the more potential energy is stored in the spring, until, well, go-go-gadget-plot-device.
Energy, formally defined, is the ability of an object to do mechanical work (we'll dig into this a few sections from now). That means anything with energy has the ability to move other objects, or create light, heat, sound—there's a whole bunch of forms energy can take.
In mechanics, we're concerned with mechanical energy (surprise), which describes the energy associated with an object's motion and position. We say that an object with the ability to move has potential energy (based on its position, it can move, but hasn't yet), while a moving object has kinetic energy; usually an object will have a mixture of both potential and kinetic energy. The other forms energy can take will come into play in later chapters, when we look at electric energy, chemical energy, radiant energy, thermal energy, and more.
Kinetic energy (K) in mechanics is the product of half an object's mass (m) and its velocity (v) squared:
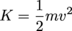
Energy is measured in units of kg⋅m2/s2, which is defined as a joule (J). It scales differently than momentum—the square in the velocity term means faster objects have much more energy than their slower counterparts.
Potential energy (U) is based on an object's position. It can come in different forms. We'll deal primarily with gravitational potential energy and spring potential energy. Gravitational potential energy is given by:
Ug = mgh
Here m is an object's mass, g is the acceleration due to gravity at the earth's surface, and h is an object's height. We can choose to place the h = 0 point anywhere that's convenient for us; gravitational potential energy is a completely relative measurement (and it's fine if it's negative, to boot).
Usually we'll choose h = 0 to be the ground, so that h is actually a height, but sometimes it makes more sense to define h = 0 to be a useful point in our problem—say, the top of a roller coaster. As long as we keep track of negative signs, this is fine.
For example, as Yoda lifts Luke's X-wing out of the Dagobah swamp he is increasing its gravitational potential energy. To determine how much gravitational potential energy Yoda gives to the X-wing, we would need to define h = 0 to be the ground. If we defined it as the surface of the swamp, we would not account for the full height Yoda has lifted it. Thus, knowing the mass and the full height Yoda lifts the X-wing, as well as the gravitational acceleration of Dagobah, determine its gravitational potential energy we can.
Spring potential energy is given by:
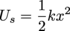
Where k is the spring's coefficient of stiffness and x is its compression distance. The more an object compresses a spring, the more potential energy is stored in the spring, until, well, go-go-gadget-plot-device.
