Energy and Momentum Terms
Center Of Mass
The point on an irregularly shaped object (or collection of objects) where the weighted sum of its mass is zero—that is, all the mass far away balances perfectly with the mass close to the center. Imagine a sumo wrestler and a horse jockey on a seesaw. You can see the center of mass is going to be much closer to the wrestler. Unless the jockey moonlights as an elephant.Conservation Law
A principle describing a mechanical quantity in a system that doesn't change no matter what you do. It's fundamental to the way the universe works; violating one is a good way to get a hefty ticket.Conservation Of Energy
Energy cannot be created nor destroyed, only transferred from one form to another. In fact, energy is to physics as glitter is to arts and crafts—you can shake it out of the bottle, you can glue it to the page, but it's still there, still glitter, and you're never, ever going to get rid of it in your living room.In mechanics, we're usually concerned with the transfer between potential energy and kinetic energy, in which case the net amount of mechanical energy is conserved. If our system isn't isolated or involves non-conservative forces, some of the energy can be transformed into heat, sound, etc. and then is no longer mechanical. Remember: total energy is conserved. Mechanical energy is only conserved if all the forces involved are conservative.
Conservation Of Momentum
Momentum can be transferred from one object to another, or from one object to many others (ever played pool?), but the total amount in an isolated system will always remain the same.Conservative And Non-Conservative Forces
Forces can be grouped into two categories, based on whether they conserve mechanical energy. In mechanics, conservative forces are those based on the position of an object, such as the force of gravity (dependent on your distance from the center of the earth) or a compressed spring (dependent on how far the spring is compressed). Non-conservative forces involve a force that adds or removes mechanical energy from a system, such as the friction between a tire and the road (turns kinetic energy into heat) or the explosion of a firecracker (turns chemical potential energy into heat, sound, kinetic energy, and singed eyebrows).Elastic And Inelastic Collisions
Collisions can be either elastic (kinetic energy is completely conserved) or inelastic (some kinetic energy is lost as sound, material deformation, etc.). In the real world, no collision is truly elastic; however, many can be treated as elastic, such as billiards balls bouncing off each other. Other collisions shouldn't be treated as elastic, such as a head-on car crash—kinetic energy is clearly not conserved, and most of the energy goes into crushing the crumple zones of the cars' hoods.Energy
The ability of an object to do work. Energy comes in many different forms—mechanical, chemical, thermal, and more—and cannot be created nor destroyed, only changed in form. The base SI unit is a joule, where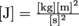 . The unit is named after James Prescott Joule, who discovered the link between heat and mechanical energy. A joule is a very small unit—1 Calorie of food energy is equivalent to over 4000 J.
. The unit is named after James Prescott Joule, who discovered the link between heat and mechanical energy. A joule is a very small unit—1 Calorie of food energy is equivalent to over 4000 J.Impulse
An object's change in momentum when a force is applied to it for any length of time, abbreviated "I.'' In formula form, I = Δp = FΔt. If an object's momentum changes suddenly, you could say it's being impulsive.Isolated System
A collection of objects we've chosen to isolate from the outside world/solar system/galaxy/universe in order to simplify our problem. Usually, this simplification doesn't change the answer at all—the influence of the moon on a terrestrial roller coaster is completely negligible, for example, so we don't include the moon in our theme park calculations.Kinetic Energy
The mechanical energy associated with a moving object, abbreviated "K.''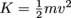 , where m is an object's mass, and v is its velocity. Kinetic energy increases as the square of speed—it takes almost as much energy to accelerate a car from 0 to 60 mph as it does to move it from 60 to 85 mph (think about that next time you're considering speeding down the highway).
, where m is an object's mass, and v is its velocity. Kinetic energy increases as the square of speed—it takes almost as much energy to accelerate a car from 0 to 60 mph as it does to move it from 60 to 85 mph (think about that next time you're considering speeding down the highway).Momentum
The product of an object's mass and velocity, abbreviated "p'' because physics always makes sense, that's why. The formula to remember is p = mv; this means momentum is in units of kilogram-meters-per-second, or, equivalently, newton-seconds. No scientist's name has been given to this unit yet, but if you write us a check we might be willing to talk to the right people for you. You know, to get the ball rolling and really give the idea some momentum.Potential Energy
The mechanical energy associated with an object's position, abbreviated "U.'' There are many different kinds of potential energy, but we'll usually be talking about gravitational potential energy (if you lift something up, it has the potential to fall) or spring potential energy (if you compress or extend a spring, it has the potential to return back to its equilibrium position). "Potential'' means no action has happened yet, but the object has the energy. It's just waiting for the right moment.Gravitational potential energy near the earth's surface can be written Ug = mgh, where m is an object's mass, g is the acceleration due to gravity (9.8 m/s2 on Earth, if you're keeping track of these things), and h is an object's height. Often we can pick the "ground level'' of a problem—that is, where h is zero—in such a way as to greatly simplify the math. As long as we're consistent with negative signs, this is a-okay.
Spring potential energy is given by
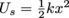 , where k is the spring's stiffness constant, and x is the compression or extension distance.
, where k is the spring's stiffness constant, and x is the compression or extension distance.Power
The rate at which an object can do mechanical work, abbreviated "P'' (this is very different than momentum, which is just "p''). It is given by the formula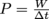 , where W is the work being done by an object in interval Δt, or by P = Fv, where F is the force an object is exerting, and v is the velocity of the body the force is being exerted on. Its SI unit is the watt, named after James Watt, a mechanical engineer who devoted much of his work to steam engines. One watt is equal to a joule per second. Power is often measured in horsepower, especially in cars and by equestrians, where 1 hp = 746 W. A car with more horsepower does more work faster, translating to faster zero-to-sixty times. A horse with more horsepower is doping like a hall of fame athlete with an asterisk.
, where W is the work being done by an object in interval Δt, or by P = Fv, where F is the force an object is exerting, and v is the velocity of the body the force is being exerted on. Its SI unit is the watt, named after James Watt, a mechanical engineer who devoted much of his work to steam engines. One watt is equal to a joule per second. Power is often measured in horsepower, especially in cars and by equestrians, where 1 hp = 746 W. A car with more horsepower does more work faster, translating to faster zero-to-sixty times. A horse with more horsepower is doping like a hall of fame athlete with an asterisk.Work
In physics, mechanical work is done any time a force moves an object—and lucky for us, the forces' union hasn't really negotiated a minimum wage yet, so we can get forces to do work all the time for pretty much free. Whenever a force F displaces an object a distance d, the work done is found by W = Fd. The unit of work is then a newton-meter, which works out to be exactly the same as a joule—the unit of energy.The Work-Energy Theorem
Work is really just a way to change a system's energy. If an outside force acts on an object and moves it, the object's kinetic energy will change—and the change in kinetic energy is exactly equal to the amount of work done by the force. We can summarize this by writing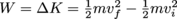 , where m is an object's mass, vi is its initial velocity, and vf is its final velocity. Work hard to remember this—it's worth the energy ba-dum, chhh).
, where m is an object's mass, vi is its initial velocity, and vf is its final velocity. Work hard to remember this—it's worth the energy ba-dum, chhh).