Test Your Knowledge
Conservation of Momentum
1. In billiards, all the numbered balls weigh 0.16 kg, but the white cue ball is slightly heavier at 0.17 kg. When a pool shark lines up a shot and sends the cue ball towards the six ball at 2 m/s, he's expecting the cue ball to rebound a bit, probably around 0.25 m/s. How fast should the six ball be traveling after the collision if he's lined his shot up perfectly?2. A drum major's baton consists of two weights at either end of a light rod, and the drum major will routinely throw the baton high into the air during marching band field shows. If the lower mass is 0.5 kg, the upper mass is 1.5 kg, and the baton is 1 m long, how far up the baton is the center of mass?
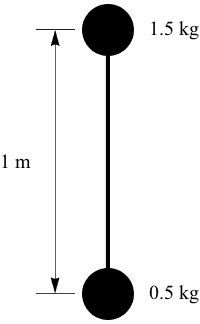
3. If the drum major throws the baton up at 3 m/s, what is the entire baton's initial momentum?
4. Which has more momentum: a 145 g baseball thrown at 30 m/s, or a 430 g soccer ball traveling at 15 m/s?
5. Johnny has a newspaper route. He delivers papers by biking around his neighborhood with a backpack full of newspapers, tossing one onto each neighbor's porch. Johnny's mass is Mj, his bike's mass is Mb, and each newspaper has a mass of m. If he pedals at a constant velocity v, what is his momentum as a function of n, the number of papers he has left to deliver?
(A) (Mj + Mb + nm)v
(B) (Mj + Mb – nm)v
(C)
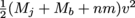
(D) (Mj + Mb)v + nm
(E) n(Mj + Mb + m)v
Impulse
1. A pool cue can transfer 30 N of force to a stationary 0.17 kg ball in 10 ms. How fast is the ball moving after the shot?2. In tennis, the ball is in contact with a player's racket for around 5 ms. If a ball (mass of 57 g) rebounds off a racket with a speed of 8 m/s, what force does the racket exert on the ball during the time of contact?
3. The space shuttle's main engines produce 2000 kN of thrust at sea level, but use 100 kg of liquid hydrogen fuel per second. A small ion thruster can produce just 500 mN of thrust in vacuum, but uses only 5 μg of fuel per second. How many times more specific impulse (impulse created per unit of fuel used) can the ion thruster create?
4. The Unstoppable Juggernaut's superpower is near limitless momentum, allowing him to crash through walls and ensuring no one makes fun of him for his doofy hat. It takes him 0.1 s to break through a concrete wall, and every wall he bursts through takes him 50 N of force. If the Juggernaut weighs 200 kg and can run at 10 m/s, how many walls would it take to stop him?
5. Imagine two pool balls rolling around on a table. Which of these could NOT change the system's momentum?
(A) A cue hitting one ball.
(B) The friction of the balls on the felt tabletop.
(C) Banging on the table.
(D) One ball hitting the other.
(E) Tilting the table.
Kinetic and Potential Energy
1. What is an object's kinetic energy (K) in terms of its momentum (p) and mass (m)?2. Which has more kinetic energy: a 145 g baseball thrown at 30 m/s, or a 430 g soccer ball traveling at 15 m/s?
3. How much potential energy is stored in a car's suspension (spring constant: 90 kN/m) when it is compressed 10 cm to make it over a speed bump?
4. How much gravitational potential energy does a skydiver (70 kg) have when he's about to jump from a plane flying at an altitude of 1200 m?
5. Every Halloween, physics students at CalTech freeze the biggest pumpkin they can find in liquid nitrogen and drop it off the library roof. What is the kinetic energy of the pumpkin when it hits the ground, in terms of its mass (m), the height of the library (h), and other fundamental constants?
Conservation of Energy
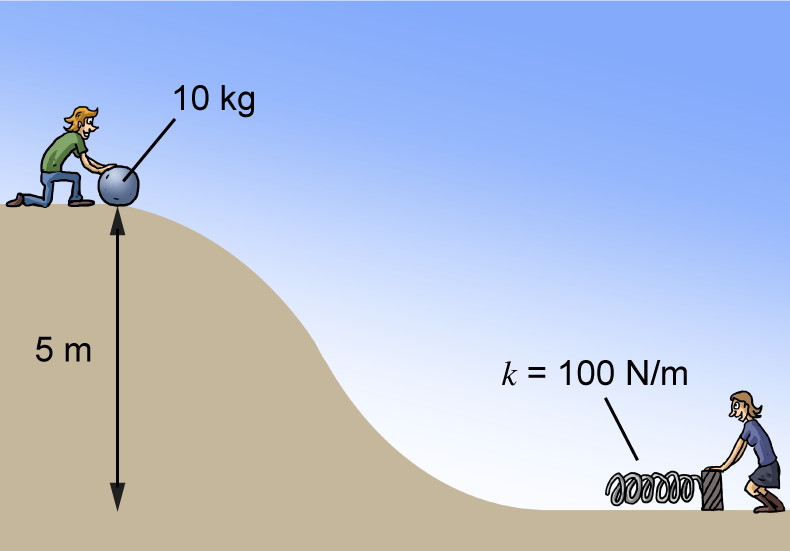
1. Imagine we release a ball of mass m from a height h. How fast is it traveling when it hits the ground? We could solve this question last chapter—using gravitational acceleration to solve the kinematics problem—but it's easier to tackle with conservation of energy.2. Jack rolls a 10 kg ball down a 5 m tall hill to Jill, who is standing at the bottom with a big spring (k = 100 N/m). How far does the spring compress in order to stop the ball?
3. Many BB guns are spring-loaded, using a compressed spring to launch little plastic pellets. How fast does a BB leave the muzzle of a spring-loaded gun? Typical plastic BBs weigh 0.2 g, and the spring (k = 400 N/m) is compressed 7 cm when the gun is cocked.
4. Six Flags is designing a new roller coaster and wants to make sure the ride goes fast. For a roller coaster car to be traveling 40 m/s at the bottom of the first drop, how tall should the drop be?
5. Another key element of roller coasters—and roller coaster design—is the loop. The minimum requirement for a roller coaster car to successfully make it through a loop on the track is that it must push against the top of the loop with a force equal to its weight. This force is called centripetal force and is dependent on the car's speed and the size of the loop, given by the formula
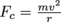 . What is the largest diameter circular loop a roller coaster can make it through if the drop is h meters high?
. What is the largest diameter circular loop a roller coaster can make it through if the drop is h meters high?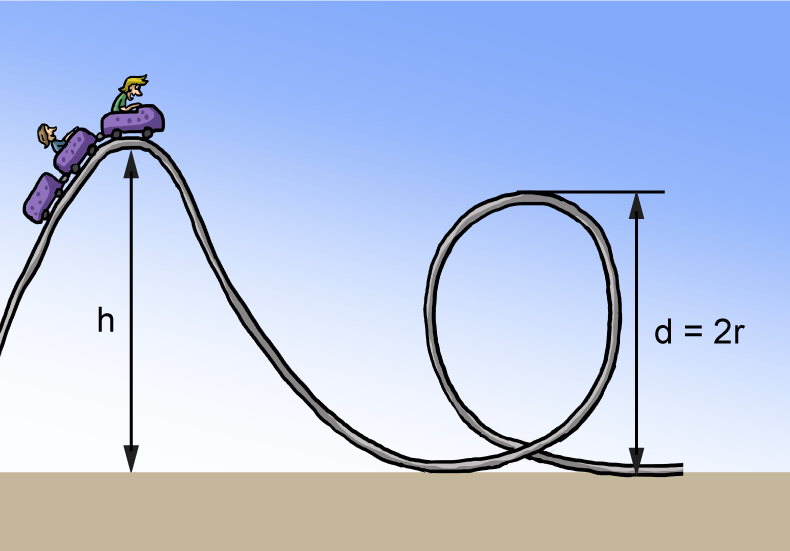
Collisions
1. Two balls (masses 5 kg and 3 kg) are rolling to the right on a table. The 5 kg ball rolls at 5 m/s and the 3 kg ball rolls at 2 m/s. After the 5 kg ball hits the 3 kg ball, what is the heavier ball's speed?2. Two pool balls (the cue ball, m = 0.17 kg, and the eight ball, m = 0.16 kg) are rolling towards each other. The cue ball is traveling at 5 m/s and the eight ball at 3 m/s. What is the eight ball's speed after they collide?
3. A basketball's coefficient of restitution is about 0.83. If it's dribbled at a speed of 6 m/s when it hits the ground, how high will it bounce?
4. Two train cars moving in the same direction are going to be coupled together. The first car weighs 5,000 kg and is moving at 5 m/s; the second weighs the same, but is moving at 1 m/s. How much kinetic energy does the system lose from coupling the cars together after they collide?
5. Prove that if a collision is elastic, the absolute value of the coefficient of restitution is 1.
Work
1. How much work does Yoda have to do to lift the 180,000 kg X-wing 10 m out of the Dagobah swamp? [Assume Dagobah is similiar in size to Earth.]2. Your best friend asks you to help her move her 100 kg table into a moving truck. You decided to apply what you have learned in physics to determine the best way to move the table. Which would take more work: lifting the table 1.5 m or pushing it 10 m across her hardwood floor with a coefficient of friction of 0.2?
3. When skateboarding, you exert a force on the ground through your foot for about a stride length (0.75 m) while trying to get the board up to speed. If you weigh 50 kg and your skateboard is moving 2 m/s before you push and 2.5 m/s after, how much force did you push off the ground with?
4. Which of the following activities takes the most work?
(A) 10 reps of bench press, lifting a 50 kg barbell 0.75 m above your chest
(B) 3 dead lifts, lifting a 100 kg barbell 1 m off the ground
(C) 2 squats, lifting a 140 kg barbell 1.25 m off the ground
(D) 15 reps of shoulder flies, lifting two 5 kg dumbbells 1 m each
(E) 15 reps of bicep curls, lifting a 40 kg barbell 0.5 m
5. Which of the following forces are NOT conservative?
(A) Gravity
(B) Friction
(C) Spring compression
(D) Air resistance
(E) Spring extension
Power
1. In the previous section, we figured out how much work Yoda did to lift the X-wing out of the Dagobah Swamp. If it took Yoda 30 s to lift the X-wing, what was his average power output while lifting?2. What about when you push the 100 kg table across a floor with a sliding friction coefficient of 0.2? If you move the table at an average speed of 1.25 m/s, what is the average power you use?
3. The sun's radiation, when it hits the earth, provides around 1300 W/m2. If a 22% efficient 3 m2 solar panel was put in the back of a 400 kg dune buggy, what's the top speed the buggy could reach? Assume the buggy is driving on dirt with a friction coefficient of 0.6 (neglect all other losses).
4. Solar power is also useful on a larger scale—imagine a field of 20,000 solar panels, each 3 m2 and 22% efficient, in the central valley of California, where solar radiation averages approximately 1300 W/m2. If the city of San Francisco has an average energy consumption of 6750 kWh per year per resident, how many people in San Francisco could get their electricity from these panels in any given year?
5. How fast can a 1000 W winch lift a 1000 kg container up to a ship's deck 7 m above the dock?
Answers
Conservation of Momentum
1. In billiards, all the numbered balls weigh 0.16 kg, but the white cue ball is slightly heavier at 0.17 kg. When a pool shark lines up a shot and sends the cue ball towards the six ball at 2 m/s, he's expecting the cue ball to rebound a bit, probably around 0.25 m/s. How fast should the six ball be traveling after the collision if he's lined his shot up perfectly?The total momentum of the system is equal to the momentum of both balls before the collision. The cue ball has (0.17 kg) × (2 m/s)=0.34 kg ⋅ m/s of momentum, while the six ball has zero momentum since it is stationary. After the collision, the cue ball has (0.17 kg) × (0.25 m/s) = 0.04 kg ⋅ m/s of momentum, so the remaining 0.30 kg ⋅ m/s must have been given to the six ball. This means the six ball's speed is
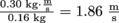 .
.2. A drum major's baton consists of two weights at either end of a light rod, and the drum major will routinely throw the baton high into the air during marching band field shows. If the lower mass is 0.5 kg, the upper mass is 1.5 kg, and the baton is 1 m long, how far up the baton is the center of mass?

The bottom of the baton is our origin. Applying the center of mass formula,
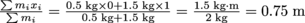 .
.3. If the drum major throws the baton up at 3 m/s, what is the entire baton's initial momentum?
The momentum of a complex object like the baton is equal to the momentum of each of its parts. pbaton = plower + pupper = (0.5 kg)(3 m/s) + (1.5 kg)(3 m/s) = 6 kg-m/s. The rod itself is light (zero mass), so it does not contribute to the baton's momentum.
4. Which has more momentum: a 145 g baseball thrown at 30 m/s, or a 430 g soccer ball traveling at 15 m/s?
The baseball has p = mv = (0.145 kg)(30 m/s) = 4.35 kg-m/s of momentum, while the soccer ball has p = (0.430 kg)(15 m/s) = 6.45 kg-m/s of momentum. The soccer ball has more momentum.
5. Johnny has a newspaper route. He delivers papers by biking around his neighborhood with a backpack full of newspapers, tossing one onto each neighbor's porch. Johnny's mass is Mj, his bike's mass is Mb, and each newspaper has a mass of m. If he pedals at a constant velocity v, what is his momentum as a function of n, the number of papers he has left to deliver?
The mass of Johnny and his bike is Mj + Mb, and is constant. Each newspaper he has left to deliver adds m to his mass, so that his total mass is Mtot = Mj + Mb + nm for n newspapers. His momentum is then p = Mtotv = (Mj + Mb + nm)v.
Impulse
1. A pool cue can transfer 30 N of force to a stationary 0.17 kg ball in 10 ms. How fast is the ball moving after the shot?The impulse given to the ball is I = Δp = FΔt = (30 N)(0.01 s) = 0.3 kg-m/s. The change in momentum of the ball is Δp = pfinal – pinitial = mvf – mvi. Since the ball's initial speed is 0 m/s, after the shot it's zipping around at a speed of
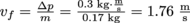 .
.2. In tennis, the ball is in contact with a player's racket for around 5 ms. If a ball (mass of 57 g) rebounds off a racket with a speed of 8 m/s, what force does the racket exert on the ball during the time of contact?
The ball is given a momentum of
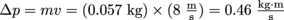 . This is equal to the impulse given to the ball from the racket, so since I = Δp = FΔt, we have
. This is equal to the impulse given to the ball from the racket, so since I = Δp = FΔt, we have 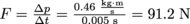 .
.3. The space shuttle's main engines produce 2000 kN of thrust at sea level, but use 100 kg of liquid hydrogen fuel per second. A small ion thruster can produce just 500 mN of thrust in vacuum, but uses only 5 μg of fuel per second. How many times more specific impulse (impulse created per unit fuel used) can the ion thruster create?
In Δt = 1 s, the space shuttle's engines create an impulse of I = FΔt = (2000 × 103 N)(1 s) = 2 × 106 kg-m/s, or
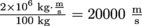 per kg of fuel. The ion thruster creates an impulse of I = (500 × 10-3 N)(1 s) = 0.5 kg-m/s, or
per kg of fuel. The ion thruster creates an impulse of I = (500 × 10-3 N)(1 s) = 0.5 kg-m/s, or 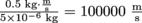 per kg of fuel. So the ion thruster can produce
per kg of fuel. So the ion thruster can produce 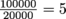 times more specific impulse.
times more specific impulse.4. The Unstoppable Juggernaut's superpower is near limitless momentum, allowing him to crash through walls and ensuring no one makes fun of him for his doofy hat. It takes him 0.1 s to break through a concrete wall, and every wall he bursts through takes him 50 N of force. If the Juggernaut weighs 200 kg and can run at 10 m/s, how many walls would it take to stop him?
The Juggernaut has 200 kg × 10 m/s = 2000 kg ⋅ m/s of momentum. If it takes him 50 N to burst through a wall, the wall must exert 50 N of force on him, as stated in Newton's third law. The reduction in momentum he feels from each wall is thus Δp = FΔt = (50 N)(0.1 s) = 5 kg ⋅ m/s. He can therefore crash through
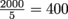 walls.
walls.5. Imagine two pool balls rolling around on a table. Which of these could NOT change the system's momentum?
Every action except one is an outside force, and those can always change the system's momentum. Choice (D) involves no outside forces—just the two balls chilling out in our system—and so the net momentum is conserved.
Kinetic and Potential Energy
1. What is an object's kinetic energy (K) in terms of its momentum (p) and mass (m)?Since p = mv,
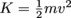 becomes
becomes 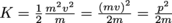 .
.2. Which has more kinetic energy: a 145 g baseball thrown at 30 m/s, or a 430 g soccer ball traveling at 15 m/s?
The baseball has
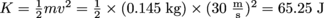 of energy, while the soccer ball has
of energy, while the soccer ball has 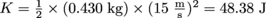 of energy. Go back to your 6th grade number line if you need to, and see that the baseball has more kinetic energy.
of energy. Go back to your 6th grade number line if you need to, and see that the baseball has more kinetic energy.3. How much potential energy is stored in a car's suspension (spring constant: 90 kN/m) when it is compressed 10 cm to make it over a speed bump?
The energy stored in a compressed spring is given by
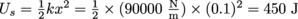 . The fun stored in a compressed spring is given by how many stairs there are nearby to send a slinky down.
. The fun stored in a compressed spring is given by how many stairs there are nearby to send a slinky down.4. How much gravitational potential energy does a skydiver (70 kg) have when he's about to jump from a plane flying at an altitude of 1200 m?
His gravitational potential energy is given by U = mgh = (70kg)(9.81 m/s2)(1200) = 824,040 kg ⋅ m2/s2 = 824,040 J. His "I'm so hyped to be jumping out of a plane" energy is off the charts, though.
5. Every Halloween, physics students at CalTech freeze the biggest pumpkin they can find in liquid nitrogen and drop it off the library roof. What is the kinetic energy of the pumpkin when it hits the ground, in terms of its mass (m), the height of the library (h), and other fundamental constants?
The pumpkin's fall is a kinematics question, its landing is a "will it look cool" question, and the aftermath is a "can we still make a pie out of it" question. The only force we'll be looking at here is the force of gravity. We can use the formula vf2 = vi2 + 2as; the initial velocity is vi = 0, so the impact velocity will be vf2 = 2as.
The displacement is the tower's height, h, and the acceleration is g, the acceleration due to gravity, giving us vf2 = 2gh. Since
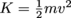 , the kinetic energy on impact is
, the kinetic energy on impact is 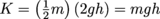 . But wait—isn't that the formula for potential energy? Almost like all of the potential energy was conserved when it was turned into kinetic energy. Yeah, almost like that.
. But wait—isn't that the formula for potential energy? Almost like all of the potential energy was conserved when it was turned into kinetic energy. Yeah, almost like that.Conservation of Energy
1. Imagine a ball of mass m we release from a height h. How fast is it traveling when it hits the ground? We could solve this question last chapter—using gravitational acceleration to solve the kinematics problem—but it's easier to tackle with conservation of energy.The ball has a gravitational potential energy of Ug = mgh, which is entirely converted into kinetic energy when it reaches ground-o-clock (h = 0). Therefore,
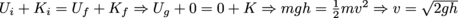 .
.2. Jack rolls a 10 kg ball down a 5 m tall hill to Jill, who is standing at the bottom with a big spring (k = 100 N/m). How far does the spring compress in order to stop the ball?

The ball has Ug = mgh = (10kg)(9.81 m/s2)(5) = 490.5 J of energy at the top of the hill. When it is stopped by the spring and is no longer moving, all of this energy has been converted into spring potential energy, so that
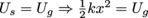 . Therefore the spring compresses a distance of
. Therefore the spring compresses a distance of 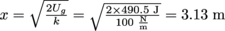 . We suggest moving out of the way of that spring, because that ball is about to book back up the hill.
. We suggest moving out of the way of that spring, because that ball is about to book back up the hill.3. Many BB guns are spring-loaded, using a compressed spring to launch little plastic pellets. How fast does a BB leave the muzzle of a spring-loaded gun? Typical plastic BBs weigh 0.2 g, and the spring (k = 400 N/m) is compressed 7 cm when the gun is cocked.
All of the spring potential energy is converted into the BB's kinetic energy:
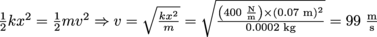 . Just be careful where you're pointing that kinetic energy; you'll put an eye out.
. Just be careful where you're pointing that kinetic energy; you'll put an eye out.4. Six Flags is designing a new roller coaster, and wants to make sure the ride goes fast. For a roller coaster car to be traveling 40 m/s at the bottom of the first drop, how tall should the drop be?
All of the car's kinetic energy will come from the potential energy it gets at the top of the chain lift, so we have
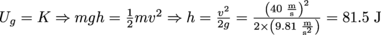 .
.5. Another key element of roller coasters—and roller coaster design—is the loop. The minimum requirement for a roller coaster car to successfully make it through a loop on the track is that it must push against the top of the loop with a force equal to its weight. This force is called centripetal force, and is dependent on the car's speed and the size of the loop, given by the formula
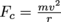 . What is the largest diameter circular loop a roller coaster can make it through if the drop is h meters high?
. What is the largest diameter circular loop a roller coaster can make it through if the drop is h meters high?
Feeling a little loopy? We hope so. The car has a total energy of Ug = mgh. When it's at the top of a loop with radius r, this energy will have been converted into both kinetic energy,
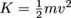 , and potential energy, Ug = mg(2r). The height of the loop is just 2r.
, and potential energy, Ug = mg(2r). The height of the loop is just 2r.The minimum force we need to avoid a Roller Coaster Tycoon-style disaster is
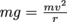 , so its minimum speed must be
, so its minimum speed must be 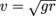 . We have
. We have 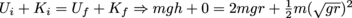 , and we can cancel out the car's mass and g to give us
, and we can cancel out the car's mass and g to give us 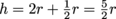 , which can be rearranged to solve for the loop's biggest possible radius,
, which can be rearranged to solve for the loop's biggest possible radius, 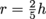 . The largest diameter loop possible, then, is
. The largest diameter loop possible, then, is 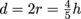 .
.Collisions
1. Two balls (masses 5 kg and 3 kg) are rolling to the right on a table. The 5 kg ball rolls at 5 m/s and the 3 kg block rolls at 2 m/s. After the 5 kg block hits the 3 kg block, what is the heavier block's speed?This is going to be an elastic collision, since all of the forces involved are in the system, so we use the elastic collision formula,
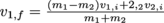 . We'll use v1,f for the final velocity of the heavier block, so plug in all our values and go for it:
. We'll use v1,f for the final velocity of the heavier block, so plug in all our values and go for it: 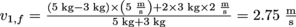 .
.2. Two pool balls (the cue ball, m = 0.17 kg, and the eight ball, m = 0.16 kg) are rolling towards each other. The cue ball is traveling at 5 m/s and the eight ball at 3 m/s. What is the eight ball's speed after they collide?
Elastic collision formula,
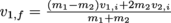 , do your thing. Since the balls are traveling in opposite directions, though, one must have a negative velocity relative to the other. Let's say it's the eight ball, which we'll also say is object 1; the magnitude of the velocity (that is, the speed) will be the same regardless of which direction we choose as positive. This gives us
, do your thing. Since the balls are traveling in opposite directions, though, one must have a negative velocity relative to the other. Let's say it's the eight ball, which we'll also say is object 1; the magnitude of the velocity (that is, the speed) will be the same regardless of which direction we choose as positive. This gives us 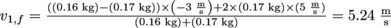 .
.3. A basketball's coefficient of restitution is about 0.83. If it's dribbled at a speed of 6 m/s when it hits the ground, how high will it bounce?
The floor the basketball is dribbled on is and always will be stationary (or at least we hope so), so its velocity will always be zero. The formula for CR will be
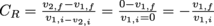 (the negative sign just means the velocity changed directions—which is the goal of dribbling). The magnitude of the basketball's rebound speed is vf = CRvi = 0.83 × (6 m/s) = 4.98 m/s.
(the negative sign just means the velocity changed directions—which is the goal of dribbling). The magnitude of the basketball's rebound speed is vf = CRvi = 0.83 × (6 m/s) = 4.98 m/s.The ball's kinetic energy after hitting the ground will be entirely converted to gravitational potential energy at the top of its bounce, giving us
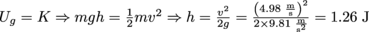 .
.4. Two train cars moving in the same direction are going to be coupled together. The first car weighs 5,000 kg and is moving at 5 m/s; the second weighs the same, but is moving at 1 m/s. How much kinetic energy does the system lose from coupling the cars together after they collide?
All aboard! This is an inelastic collision, but momentum is still conserved:
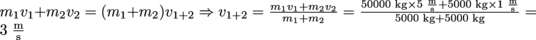 . The kinetic energy of the cars before the collision is
. The kinetic energy of the cars before the collision is 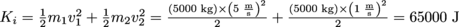 , and their kinetic energy after they couple together is
, and their kinetic energy after they couple together is  . So, after coupling, the cars lose 20,000 J of energy.
. So, after coupling, the cars lose 20,000 J of energy.5. Prove that if a collision is elastic, the absolute value of the coefficient of restitution is 1.
If a collision is elastic, we know v1,f and v2,f in terms of m1, m2, v1,i and v2,i. That, and the formula for the coefficient of restitution, is all we need.
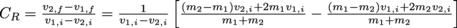 . That's a bit of a mess (understatement: that's a lot of a mess), so let's simplify.
. That's a bit of a mess (understatement: that's a lot of a mess), so let's simplify.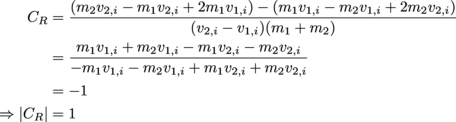
Work
1. How much work does Yoda have to do to lift the 180,000 kg X-wing 10 m out of the Dagobah swamp? [Assume Dagobah is similiar in size to Earth.]The force required to lift the X-wing is equal to its weight Fg = mg = (180,000 kg)(9.81 m/s2) = 1,765,800 N. Thus the work Yoda does to lift the X-wing is W = Fgd = (1,765,800 N)(10 m)= 17,658,000 J. This is about twice the recommended food energy required for an average person in a day, which Yoda burns in seconds.
2. Your best friend asks you to help her move her 100 kg table into a moving truck. You decided to apply what you have learned in physics to determine the best way to move the table. Which would take more work: lifting the table 1.5 m or pushing it 10 m across her hardwood floor with a coefficient of friction of 0.2?
To lift the table you would have to counteract the force of gravity Fg = mg = (100kg)(9.81 m/s2) = 981 N. Thus the work to lift the table is W = Fgd = (981 N)(1.5 m)=1472 J. To push the table, the force you're moving is the frictional resistance of the floor on the table, Ff = μmg = 0.2(100kg)(9.81 m/s2) = 196 N. The work you're doing this time around is W = Ffd = (196 N)(10 m) = 1960 J. In conclusion, it would depend on how much pizza your friend is supplying, one slice is about 1600 Joules.
3. When skateboarding, you exert a force on the ground through your foot for about a stride length (0.75 m) while trying to get the board up to speed. If you weigh 50 kg and your skateboard is moving 2 m/s before you push and 2.5 m/s after, how much force did you push off the ground with?
We can't go from all the information given to us straight to the amount of force. First, we need to see how much work we did. Using the work-energy theorem,
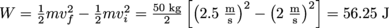 . Since W = Fd, the amount of force used to get to shredding speed is
. Since W = Fd, the amount of force used to get to shredding speed is 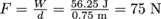 .
.4. Which of the following activities takes the most work?
All of the answer choices are variations of W = Fd:
(A) W= 10(50kg)(0.75) = 375
(B) W = 3(100kg)(1) = 300
(C) W = 2(140)(1.25) = 350
(D) W = 15(2)(5kg)(1) = 150
(E) W = 15(40kg)(0.5) = 300
Choice (A) takes the most work, so it also takes the cake.
5. Which of the following forces are NOT conservative?
Conservative forces are based on an object's position. Friction (B) and air resistance (D) are independent of position, and so they are non-conservative.
Power
1. In the previous section, we figured out how much work Yoda did to lift the X-wing out of the Dagobah Swamp. If it took Yoda 30 s to lift the X-wing, what was his average power output while lifting?Power is the amount of work performed during a duration of time. You should have discovered that Yoda does 17,658,000 J of work. Thus, his Power output is 17,658,000 J / 30 s = 588,600 Watts or 1.5 times the power output of an 18-wheeler truck engine.
2. What about when you push the 100 kg table across a floor with a sliding friction coefficient of 0.2? If you move the table at an average speed of 1.25 m/s, what is the average power you use?
We've got a different power formula this time, P = Fv. Changing Fv into a slightly handier form, plugging away, and simplifying, gets us P = μmgv = 0.2(100kg)(9.81 m/s2)(1.25 m/s) = 245.3 W.
3. The sun's radiation, when it hits the earth, provides around 1300 W/m2. If a 22% efficient 3 m2 solar panel was put in the back of a 400 kg dune buggy, what's the top speed the buggy could reach? Assume the buggy is driving on dirt with a friction coefficient of 0.6 (neglect all other losses).
The solar panel can provide a power of
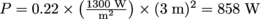 to the buggy. Rearranging P = Fv gives us
to the buggy. Rearranging P = Fv gives us 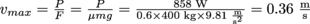 , or a blazing 0.8 mph. This is why solar-powered cars aren't really a thing yet.
, or a blazing 0.8 mph. This is why solar-powered cars aren't really a thing yet.4. Solar power is also useful on a larger scale—imagine a field of 20,000 solar panels, each 3 m2 and 22% efficient, in the central valley of California, where solar radiation averages approximately 1300 W/m2. If the city of San Francisco has an average energy consumption of 6750 kWh per year per resident, how many people in San Francisco could get their electricity from these panels in any given year?
Each SF resident uses 6750 kWh of energy per year, or
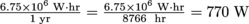 of power on average in any given second. Our solar farm can provide
of power on average in any given second. Our solar farm can provide 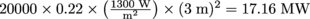 of power—that means it can provide electricity to
of power—that means it can provide electricity to 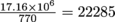 people in San Francisco.
people in San Francisco.5. How fast can a 1000 W winch lift a 1000 kg container up to a ship's deck 7 m above the dock?
The winch is doing W = Fd = mgd = (1000kg)(9.81 m/s2)(7) = 68,670 J of work. If it has a 1000 W motor, it can do that amount of work in
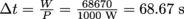 . That's quite a bit faster than we could do it; we'll leave the 1+ ton weights to the winch.
. That's quite a bit faster than we could do it; we'll leave the 1+ ton weights to the winch.