Density
Now that we know to think of fluids as being continuous, we'll define certain properties that exist in the real world: a world where a drop of water is a drop of water and isn't made up of 3 × 1021 atoms. We call this "real world" scale the macroscopic scale.
The first property we need to understand is density.
According to Greek mythology, the goddess of discord was called Eris. One day she got mad because her invitation to Zeus' latest garden party got "lost in the mail." Know what she did? She threw a golden apple in Zeus' garden. The golden apple was inscribed with the words ΤΗΙ ΚΑΛΛΙΣΤΗΙ, which translates as TO THE MOST BEAUTIFUL.
Yep, we can guess what happened. Three goddesses claimed the apple: Hera, Athena, and Aphrodite. This, by the way, is what eventually caused the Trojan War.
No, this section on density isn't turning into a beauty pageant. We have an idea of what a typical apple's average mass and size is like, and how "solid" an apple feels. Eris' golden apple, though, would weigh a lot more. Why is that?
It would weigh more because the golden apple has a higher density than the normal apple. That's it.
The higher the weight for objects of the same size, the higher the density. That tells us that the density of an object depends on weight and size. Weight and size aren't very specific terms, though, and we like specifics. Let's change it a little, we know that weight is a measurement of mass, and we know that size is the amount of volume something takes. That means that density depends on mass and volume.
Mass and volume, huh?
Yes, mass and volume. Since a higher volume corresponds to a higher mass with the same density, the density is inversely proportional to the volume. With that, we know everything we need to know in order to define density. Let's do it.
First, let's assign density the Greek letter ρ, rho, pronounced "row." We're running out of English letters with all these physics formulas. Using the logic above and a little bit of math, we can write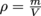 , density equals the mass of an object divided by its volume. Density has units of
, density equals the mass of an object divided by its volume. Density has units of 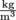 in standard international units, but is commonly expressed in
in standard international units, but is commonly expressed in 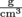 as well. This form is handy when volume is in milliliters, because 1 ml = 1 cm3, otherwise known as 1 cc.
as well. This form is handy when volume is in milliliters, because 1 ml = 1 cm3, otherwise known as 1 cc.
If the density of a standard apple is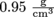 and the volume of an especially big apple is 500 cm3, we can find the mass from
and the volume of an especially big apple is 500 cm3, we can find the mass from 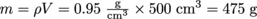 .
.
Unfortunately, specific gravity has nothing to do with gravity. The specific gravity of a fluid is simply its density divided by the density of water at 4 °C, which is the temperature at which water is its most dense. At this temperature, water has a density of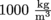 . It's not much less at other temperatures, though.
. It's not much less at other temperatures, though.
We just learned that density is mass over volume. It turns out that there is also a term for the inverse of density. We call the inverse of density specific volume, and give it the Greek symbol ν, pronounced nu. Since density is mass divided by volume, specific volume is volume divided by mass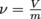 and specific volume has the inverse units of density,
and specific volume has the inverse units of density, 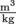 for SI units. The specific volume of that apple with a density of
for SI units. The specific volume of that apple with a density of 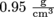 is
is 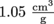 . Not that that's in standard units, but we get the idea.
. Not that that's in standard units, but we get the idea.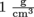 , densities less than 1 float, and higher than 1 sink. That's the bottom line. Don't drop it. Oh, and watch those units. Compatibility is the key, and also don't forget that to convert from cubic meters to cubic centimeters requires multiplying by 100,000, not 100.
, densities less than 1 float, and higher than 1 sink. That's the bottom line. Don't drop it. Oh, and watch those units. Compatibility is the key, and also don't forget that to convert from cubic meters to cubic centimeters requires multiplying by 100,000, not 100.
The first property we need to understand is density.
According to Greek mythology, the goddess of discord was called Eris. One day she got mad because her invitation to Zeus' latest garden party got "lost in the mail." Know what she did? She threw a golden apple in Zeus' garden. The golden apple was inscribed with the words ΤΗΙ ΚΑΛΛΙΣΤΗΙ, which translates as TO THE MOST BEAUTIFUL.
Yep, we can guess what happened. Three goddesses claimed the apple: Hera, Athena, and Aphrodite. This, by the way, is what eventually caused the Trojan War.
No, this section on density isn't turning into a beauty pageant. We have an idea of what a typical apple's average mass and size is like, and how "solid" an apple feels. Eris' golden apple, though, would weigh a lot more. Why is that?
It would weigh more because the golden apple has a higher density than the normal apple. That's it.
The higher the weight for objects of the same size, the higher the density. That tells us that the density of an object depends on weight and size. Weight and size aren't very specific terms, though, and we like specifics. Let's change it a little, we know that weight is a measurement of mass, and we know that size is the amount of volume something takes. That means that density depends on mass and volume.
Mass and volume, huh?
Yes, mass and volume. Since a higher volume corresponds to a higher mass with the same density, the density is inversely proportional to the volume. With that, we know everything we need to know in order to define density. Let's do it.
First, let's assign density the Greek letter ρ, rho, pronounced "row." We're running out of English letters with all these physics formulas. Using the logic above and a little bit of math, we can write
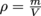 , density equals the mass of an object divided by its volume. Density has units of
, density equals the mass of an object divided by its volume. Density has units of 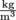 in standard international units, but is commonly expressed in
in standard international units, but is commonly expressed in 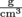 as well. This form is handy when volume is in milliliters, because 1 ml = 1 cm3, otherwise known as 1 cc.
as well. This form is handy when volume is in milliliters, because 1 ml = 1 cm3, otherwise known as 1 cc.If the density of a standard apple is
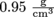 and the volume of an especially big apple is 500 cm3, we can find the mass from
and the volume of an especially big apple is 500 cm3, we can find the mass from 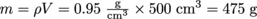 .
.Specific Gravity and Specific Volume
To wrap our brilliant minds around density, it helps to compare the density of a new fluid with the density of a fluid with which we are very familiar like…water. That's right, plain old H20 is a great candidate for the job. We all know what water feels like, what it behaves like, and how it makes the perfect wake-up device, but let's talk about the specifics of water. Ever heard the term specific gravity?Unfortunately, specific gravity has nothing to do with gravity. The specific gravity of a fluid is simply its density divided by the density of water at 4 °C, which is the temperature at which water is its most dense. At this temperature, water has a density of
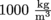 . It's not much less at other temperatures, though.
. It's not much less at other temperatures, though.We just learned that density is mass over volume. It turns out that there is also a term for the inverse of density. We call the inverse of density specific volume, and give it the Greek symbol ν, pronounced nu. Since density is mass divided by volume, specific volume is volume divided by mass
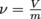 and specific volume has the inverse units of density,
and specific volume has the inverse units of density, 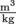 for SI units. The specific volume of that apple with a density of
for SI units. The specific volume of that apple with a density of 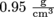 is
is 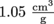 . Not that that's in standard units, but we get the idea.
. Not that that's in standard units, but we get the idea.Common Mistakes
On the scale of water having a density of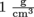 , densities less than 1 float, and higher than 1 sink. That's the bottom line. Don't drop it. Oh, and watch those units. Compatibility is the key, and also don't forget that to convert from cubic meters to cubic centimeters requires multiplying by 100,000, not 100.
, densities less than 1 float, and higher than 1 sink. That's the bottom line. Don't drop it. Oh, and watch those units. Compatibility is the key, and also don't forget that to convert from cubic meters to cubic centimeters requires multiplying by 100,000, not 100.