Fluid Dynamics
We started this unit by defining a fluid as any matter that flows when a force is applied to it. This includes amorphous solids in addition to liquids and gases. Then we began an exploration of fluids on a macroscopic scale and discussed several cases of hydrostatic equilibrium. What happens when a fluid flows on a microscopic scale?
To analyze flow, we are going to simplify again by introducing two new terms: ideal fluid and viscosity.
An ideal fluid is a fluid that behaves in a certain way, just as an ideal gas behaves in a certain way. Ideal fluids are well mannered.
The properties that make a fluid "ideal" are viscosity and compressibility. We'll talk about viscosity in the next paragraph, but we introduced compressibility when we talked about how to liquefy a gas. We also defined a liquid as being more or less incompressible, which tells us its density cannot change. Keep this in mind.
Back to viscosity. When we picture something viscous, we picture something like molasses and slimy aliens (probably like the one who abducted you earlier on). Viscosity is exactly that. Something viscous, like molasses or alien slime, takes a while to get anywhere. (Feel free to pop into a sci-fi movie to be reminded. When is an alien NOT slimy? Forget E.T.)
In physics, viscosity is a measure of internal friction between molecules. We already know what friction is from Newtonian mechanics. When we skate, there is very little friction between our skates and the ice, so we slide. Try sliding with running shoes on the street—chances are we're not sliding anywhere—the same thing happens with the molecules of really viscous fluids.
So, in terms of viscosity, we say that the higher the viscosity, the higher the internal friction, and the higher the friction, the slower a fluid moves.
We are ready to define an ideal fluid as a fluid that has zero compressibility and zero viscosity. In the following discussion, we may assume that all fluids are ideal with no changes in density and no internal friction. It sounds too ideal, because it is.
He's back. Kind of.
As we recall Archimedes running around naked, we'll remember he measured a crown's volume by measuring how much water the crown displaced out of a container. Water flowed. That brings us to our next point, the motion of a fluid is called flow. Not very surprising, we know.
We already know water is made up of molecules, and these molecules are composed of particles. As water flows in a pipeline, for instance, water molecules rush from one end to the other, which means subatomic particles are rushing from one end to the other. We call the path that every particle follows a flow line. If we choose to examine a particular section of the pipeline, we end up with a "tube-looking thing" in which water flows. This tube-looking thing is called a flow tube. Let's look at this diagram so we don't get too confused.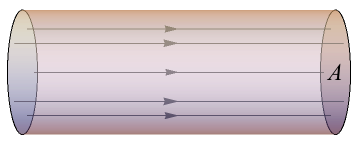 Here we see flow lines flowing through the area of a flow tube. (No, this isn't a pronunciation exercise, but try adding "fluid" in there just for fun and we become Eliza Doolittle in My Fair Lady).
Here we see flow lines flowing through the area of a flow tube. (No, this isn't a pronunciation exercise, but try adding "fluid" in there just for fun and we become Eliza Doolittle in My Fair Lady).
What happens when the flow tube narrows? A picture is worth a thousand words. Let's examine this closely.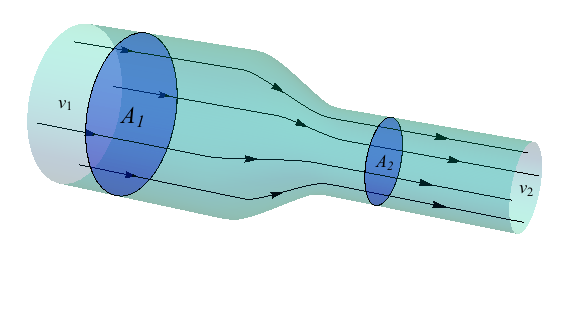 We can see how flow lines now flow pass through different areas A1 and A2 and different velocities v1 and v2.
We can see how flow lines now flow pass through different areas A1 and A2 and different velocities v1 and v2.
Question: In the above diagram, is v1 higher or lower than v2?
Unless someone has magical powers we don't know about, the quantity of water flowing through the flow tube doesn't miraculously change. The flow rate is constant, regardless of what cross-sectional area it's traveling through. Above we see A2 is less than A1. We don't know yet the difference in speed or rate of flow through these respective areas.
Imagine that tube filled with ants from wall to wall. For the same number of ants to pass any vertical line over the same time interval, ants have to move faster in the narrow section than the wide section, so v1 is lower than v2 in our diagram. Whenever a fluid flows (there we go again with our My Fair Lady enunciation exercises), the mass, density, and volume of that fluid are constant and contained, so the flow rate is constant.
Let's say this together: The fluid in a flow tube stays always in the flow tube.
So, apart from rewording musicals, where does this bring us?
It brings us to the conservation law of mass, or conservation law of ants, which states that if you start off with a certain number of ants crossing over a tunnel over some specified time interval, the exact same amount will come out at the end of the tunnel for the same time interval (not taking into account a clumsy observer or a water spider). No ants (or anything with mass) will be harmed in the production of science experiments—thanks universe. As the area shrinks, both ants and water have to go faster to maintain the same flow rate, but hey, that's ok.
How do we express this constant flow mathematically? Let's derive it. A uniform line implies a constant density—our friend ρ is back—where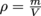 .
.
We already stated that m stays constant, so a constant density implies the volume of the ants crossing A1 has to equal the volume of ants crossing A2.
Volume in terms of area A1 is V1 = length l × A1, where length is given by l = v1 × t, where v is velocity and t is time. The volume can be written as V1 = A1v1t. Using the same logic, then we can also write V2 = A2v2t.
For a constant density (with a compressibility of 0), the volumes are equivalent, or V1 = V2. We can write that V1 = A1v1t = V2 = A2v2t. Time cancels out, and we are left with an equation called the continuity equation: A1v1 = A2v2.
The product Av, by the way, is known in physics as the volume flow rate. The units of the volume flow rate are m2 ×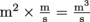 . We can convert metric volume units m3 into liter because there are 1000 liters in 1 cubic meter, so flow rate is often measured in liters per second.
. We can convert metric volume units m3 into liter because there are 1000 liters in 1 cubic meter, so flow rate is often measured in liters per second.
Remember that this relationship came about while assuming a constant number of ants over a time interval, constant number of ants = constant density. A constant density also means that a fluid is incompressible, as we've mentioned before. Just to hammer it home, the above continuity equation is only applicable for an incompressible fluid.
Let's practice: what's the cross-sectional area of a tube where a fluid flows at 0.5 if in a section with an area of 5 cm2 the speed is 1.5
if in a section with an area of 5 cm2 the speed is 1.5  ?
?
First, we need to convert the area into SI units, so A2 = 0.0005 m2 because we have to divide by 100 twice for area, as opposed to once for distance. Then we use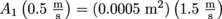 , so A1 = 0.0015 m2, which is 15 cm2.
, so A1 = 0.0015 m2, which is 15 cm2.
If we compare the two areas and the two speeds, we see that the first area is three times higher than the second area, while the second has a speed three times that of the first area. That makes sense because we could alternatively express the continuity equation in terms of ratios: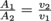 .
.
Bad news first. This new section has the most complicated derivation of this module so far, but the good news is it's the last derivation. The other good news is that as always, we're here to simplify the process. One more good news: at the end of this, we'll be able to explain how airplanes work. More or less.
In the continuity equation, A1v1 = A2v2, we described how the velocity of a fluid varies as it travels through a flow tube. We defined flow rate as the product of an area times the velocity, Av. We've also talked about how the pressure of a fluid varies at different heights, P = Po + ρgh. How do we combine pressure, height, and flow rate?
The guy in the fancy wig, Isaac Newton, liked to say that F = ma. We know a change in velocity, like going from v1 to v2, is the veritable definition of acceleration. While crossing from A1 to A2, our fluid accelerates with a constant force F. If there's no force, the fluid doesn't accelerate since they're attached to each other by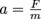 and the mass of the fluid doesn't evaporate away: it's in a sealed tube (as far as we know).
and the mass of the fluid doesn't evaporate away: it's in a sealed tube (as far as we know).
Where does this force come from?
There are forces here that we don't care about, namely, the forces that cancel each other out like the normal force and gravity. The fluid doesn't explode out of the tube. Any force that is not in the direction of flow is irrelevant. Ignore those ones. Forget they exist. All we care about is the force behind that motion, both literally and figuratively. How often can we say that and mean it?
The force behind a fluid's acceleration isthe fluid itself. Think of the ants: they are in continuous motion and aren't allowed to stop walking. They are pushed by the other ants behind them.
And where does pressure fit in here? Well, we know pressure is given by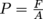 . Since a fluid feels the same force while crossing different cross-sectional areas, then what can we finally shout out at the top of a mountain?
. Since a fluid feels the same force while crossing different cross-sectional areas, then what can we finally shout out at the top of a mountain?
That's right. The pressure that a fluid feels crossing a smaller area is higher. We could have guessed this too, since pressure is inversely proportional to area.
The point is, however, that it would be impossible for a fluid to rush towards an area of higher pressure. It would have to decelerate to compensate, and once a fluid gets going, it doesn't slow down for anything unless forced to.
Okay…so we might've been tricked into reviewing a concept from a different angle, but it's for a good cause.. To deliver the promised relation between height, flow rate, and pressure, we have to look at three things, which we've already read about in Shmoop: work, energy, and work & energy.
Together, work, energy, and work & energy make up the work-energy theorem.
Kinetic energy of an object (or fluid) is given by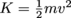 . The difference of kinetic energies that the fluid feels in our tube between areas A1 and A2 is given by
. The difference of kinetic energies that the fluid feels in our tube between areas A1 and A2 is given by 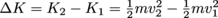 .
.
This change in kinetic energy is equal to the work done on the fluid by the work-energy theorem.
Work is defined as force times distance, and we can separate out the work done in different directions: W = Wx + Wy = Fx1 x1 + Fx2 x2 + Fy1 y1 + Fy2 y2. The following diagram will help, as diagrams do.
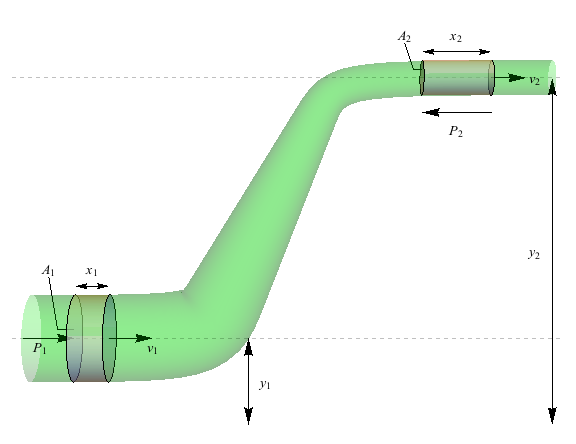
There's *gasp* a height difference in these sections of pipe. No need to panic, because potential energy is true for pipes, and we can separate out the horizontal forces from the vertical ones and then add them back together at the end.
Let's start with the x-direction, without a height increase. The fluid under pressure P1 travels through area A1 at a velocity v1 and crosses a distance of x1.
This means the first term of our work equation, Fx1 x1, is given by P1 A1 x1 because force is related to pressure by F = PA. And what is area times length (A1 x1)? Volume V1.
We may simplify the first term to P1V1.
The second term in the x-direction is the same with 2's in it, only we have to remember that force is a vector. Because the fluid goes from having velocity v1 to v2, we determined the fluid accelerates. However, Isaac Newton clearly insisted that an object always resists a change in velocity (the couch potato law), so Fx2 actually opposes this change in velocity. Mathematically, we add a negative sign to Fx2. All together, Wx then equals P1V1 − P2V2.
We can also think about this as negative work .
Sighs of relief and high fives; we've figured out that Wx = P1V1 – P2V2.
What about the y-direction? We turn our attention now to Wy. The only force in this direction is gravity (W = F = -mg). As the fluid rises by a height of the difference of y2 – y1, gravity does negative work such that Wy = -mg (y2 – y1). The fluid has to fight the force of gravity, but that's it.
Our entire equation can then be written as W = P1V1 – P2V2 + mgy1 – mgy2.
Going back to the work-energy theorem, we can fill in some blanks.
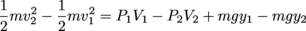
We next isolate the 1's and 2's:
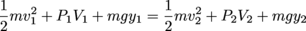
Since m = ρV is in terms of density and volume, we finally, finally get Bernoulli's equation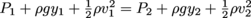 , or
, or 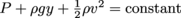 .
.
Whew! We did it. Shall we take it for a test drive? Nah. We'll take a break first and practice later.
Believe it or not, Bernoulli's equation lays the foundation of how airplanes function, amongst other things.
Lift, as in air lift, is explained as a difference of pressure. Air molecules have a higher velocity when they fly over the curved side of an airplane wing because of the greater distance: those air molecules have further to go to meet up at the other side with the ones who pass under the straight side of the wing. The pressure of air depends on the velocity of its particles, so the pressure above the wing is less than the pressure below. In essence, the high pressure at the bottom of the wing is what creates lift, which is essential for the flight of airplanes.
The following diagram shows how lift works:
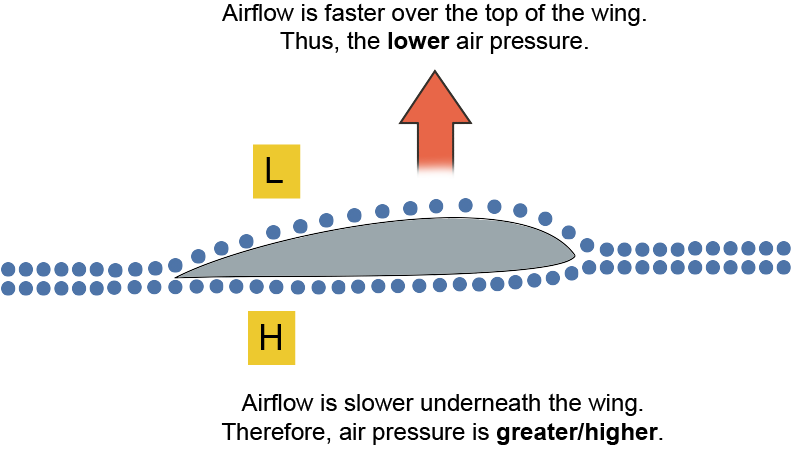
Okay, now we'll try out Bernoulli's equation for ourselves.
A pipe ascends vertically for 8 feet, or 2.3 m. The velocity of the water at both top and bottom of the pipe is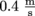 , and as usual the density is
, and as usual the density is 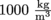 . The pressure at the top is open to the atmosphere because it's coming out of a faucet. What's the pressure at the bottom?
. The pressure at the top is open to the atmosphere because it's coming out of a faucet. What's the pressure at the bottom?
Let's look at the equation and see what else we know: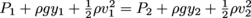 . We're looking for P1, and we know that P2 is atmospheric pressure, which is 1.01 × 105 Pa. We may call y1 zero and y2 = 2.3 m. The velocity terms are identical on both sides of the equation because velocity is constant so they cancel each other out, and we know ρ and g.
. We're looking for P1, and we know that P2 is atmospheric pressure, which is 1.01 × 105 Pa. We may call y1 zero and y2 = 2.3 m. The velocity terms are identical on both sides of the equation because velocity is constant so they cancel each other out, and we know ρ and g.
This leads to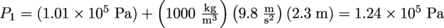 . Gauge pressure, as before, just subtracts atmospheric pressure, or 22,540 Pa. Not that we were asked. We like to go above and beyond the call at duty sometimes, just to shake things up.
. Gauge pressure, as before, just subtracts atmospheric pressure, or 22,540 Pa. Not that we were asked. We like to go above and beyond the call at duty sometimes, just to shake things up.
Ideal Fluid
Unless we feel like spending the rest of our lives analyzing the various currents encountered during our next white water rafting expedition, we need to simplify things once again.To analyze flow, we are going to simplify again by introducing two new terms: ideal fluid and viscosity.
An ideal fluid is a fluid that behaves in a certain way, just as an ideal gas behaves in a certain way. Ideal fluids are well mannered.
The properties that make a fluid "ideal" are viscosity and compressibility. We'll talk about viscosity in the next paragraph, but we introduced compressibility when we talked about how to liquefy a gas. We also defined a liquid as being more or less incompressible, which tells us its density cannot change. Keep this in mind.
Back to viscosity. When we picture something viscous, we picture something like molasses and slimy aliens (probably like the one who abducted you earlier on). Viscosity is exactly that. Something viscous, like molasses or alien slime, takes a while to get anywhere. (Feel free to pop into a sci-fi movie to be reminded. When is an alien NOT slimy? Forget E.T.)
In physics, viscosity is a measure of internal friction between molecules. We already know what friction is from Newtonian mechanics. When we skate, there is very little friction between our skates and the ice, so we slide. Try sliding with running shoes on the street—chances are we're not sliding anywhere—the same thing happens with the molecules of really viscous fluids.
So, in terms of viscosity, we say that the higher the viscosity, the higher the internal friction, and the higher the friction, the slower a fluid moves.
We are ready to define an ideal fluid as a fluid that has zero compressibility and zero viscosity. In the following discussion, we may assume that all fluids are ideal with no changes in density and no internal friction. It sounds too ideal, because it is.
Continuity Equation
Remember the naked guy who shouted "Eureka!"?He's back. Kind of.
As we recall Archimedes running around naked, we'll remember he measured a crown's volume by measuring how much water the crown displaced out of a container. Water flowed. That brings us to our next point, the motion of a fluid is called flow. Not very surprising, we know.
We already know water is made up of molecules, and these molecules are composed of particles. As water flows in a pipeline, for instance, water molecules rush from one end to the other, which means subatomic particles are rushing from one end to the other. We call the path that every particle follows a flow line. If we choose to examine a particular section of the pipeline, we end up with a "tube-looking thing" in which water flows. This tube-looking thing is called a flow tube. Let's look at this diagram so we don't get too confused.

What happens when the flow tube narrows? A picture is worth a thousand words. Let's examine this closely.

Question: In the above diagram, is v1 higher or lower than v2?
Unless someone has magical powers we don't know about, the quantity of water flowing through the flow tube doesn't miraculously change. The flow rate is constant, regardless of what cross-sectional area it's traveling through. Above we see A2 is less than A1. We don't know yet the difference in speed or rate of flow through these respective areas.
Imagine that tube filled with ants from wall to wall. For the same number of ants to pass any vertical line over the same time interval, ants have to move faster in the narrow section than the wide section, so v1 is lower than v2 in our diagram. Whenever a fluid flows (there we go again with our My Fair Lady enunciation exercises), the mass, density, and volume of that fluid are constant and contained, so the flow rate is constant.
Let's say this together: The fluid in a flow tube stays always in the flow tube.
So, apart from rewording musicals, where does this bring us?
It brings us to the conservation law of mass, or conservation law of ants, which states that if you start off with a certain number of ants crossing over a tunnel over some specified time interval, the exact same amount will come out at the end of the tunnel for the same time interval (not taking into account a clumsy observer or a water spider). No ants (or anything with mass) will be harmed in the production of science experiments—thanks universe. As the area shrinks, both ants and water have to go faster to maintain the same flow rate, but hey, that's ok.
How do we express this constant flow mathematically? Let's derive it. A uniform line implies a constant density—our friend ρ is back—where
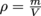 .
.We already stated that m stays constant, so a constant density implies the volume of the ants crossing A1 has to equal the volume of ants crossing A2.
Volume in terms of area A1 is V1 = length l × A1, where length is given by l = v1 × t, where v is velocity and t is time. The volume can be written as V1 = A1v1t. Using the same logic, then we can also write V2 = A2v2t.
For a constant density (with a compressibility of 0), the volumes are equivalent, or V1 = V2. We can write that V1 = A1v1t = V2 = A2v2t. Time cancels out, and we are left with an equation called the continuity equation: A1v1 = A2v2.
The product Av, by the way, is known in physics as the volume flow rate. The units of the volume flow rate are m2 ×
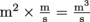 . We can convert metric volume units m3 into liter because there are 1000 liters in 1 cubic meter, so flow rate is often measured in liters per second.
. We can convert metric volume units m3 into liter because there are 1000 liters in 1 cubic meter, so flow rate is often measured in liters per second. Remember that this relationship came about while assuming a constant number of ants over a time interval, constant number of ants = constant density. A constant density also means that a fluid is incompressible, as we've mentioned before. Just to hammer it home, the above continuity equation is only applicable for an incompressible fluid.
Let's practice: what's the cross-sectional area of a tube where a fluid flows at 0.5
 if in a section with an area of 5 cm2 the speed is 1.5
if in a section with an area of 5 cm2 the speed is 1.5  ?
?First, we need to convert the area into SI units, so A2 = 0.0005 m2 because we have to divide by 100 twice for area, as opposed to once for distance. Then we use
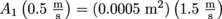 , so A1 = 0.0015 m2, which is 15 cm2.
, so A1 = 0.0015 m2, which is 15 cm2. If we compare the two areas and the two speeds, we see that the first area is three times higher than the second area, while the second has a speed three times that of the first area. That makes sense because we could alternatively express the continuity equation in terms of ratios:
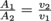 .
.Bernoulli's Equation
We have some good news and some bad news.Bad news first. This new section has the most complicated derivation of this module so far, but the good news is it's the last derivation. The other good news is that as always, we're here to simplify the process. One more good news: at the end of this, we'll be able to explain how airplanes work. More or less.
In the continuity equation, A1v1 = A2v2, we described how the velocity of a fluid varies as it travels through a flow tube. We defined flow rate as the product of an area times the velocity, Av. We've also talked about how the pressure of a fluid varies at different heights, P = Po + ρgh. How do we combine pressure, height, and flow rate?
The guy in the fancy wig, Isaac Newton, liked to say that F = ma. We know a change in velocity, like going from v1 to v2, is the veritable definition of acceleration. While crossing from A1 to A2, our fluid accelerates with a constant force F. If there's no force, the fluid doesn't accelerate since they're attached to each other by
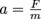 and the mass of the fluid doesn't evaporate away: it's in a sealed tube (as far as we know).
and the mass of the fluid doesn't evaporate away: it's in a sealed tube (as far as we know). Where does this force come from?
There are forces here that we don't care about, namely, the forces that cancel each other out like the normal force and gravity. The fluid doesn't explode out of the tube. Any force that is not in the direction of flow is irrelevant. Ignore those ones. Forget they exist. All we care about is the force behind that motion, both literally and figuratively. How often can we say that and mean it?
The force behind a fluid's acceleration isthe fluid itself. Think of the ants: they are in continuous motion and aren't allowed to stop walking. They are pushed by the other ants behind them.
And where does pressure fit in here? Well, we know pressure is given by
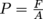 . Since a fluid feels the same force while crossing different cross-sectional areas, then what can we finally shout out at the top of a mountain?
. Since a fluid feels the same force while crossing different cross-sectional areas, then what can we finally shout out at the top of a mountain? That's right. The pressure that a fluid feels crossing a smaller area is higher. We could have guessed this too, since pressure is inversely proportional to area.
The point is, however, that it would be impossible for a fluid to rush towards an area of higher pressure. It would have to decelerate to compensate, and once a fluid gets going, it doesn't slow down for anything unless forced to.
Okay…so we might've been tricked into reviewing a concept from a different angle, but it's for a good cause.. To deliver the promised relation between height, flow rate, and pressure, we have to look at three things, which we've already read about in Shmoop: work, energy, and work & energy.
Together, work, energy, and work & energy make up the work-energy theorem.
Kinetic energy of an object (or fluid) is given by
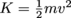 . The difference of kinetic energies that the fluid feels in our tube between areas A1 and A2 is given by
. The difference of kinetic energies that the fluid feels in our tube between areas A1 and A2 is given by 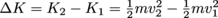 .
.This change in kinetic energy is equal to the work done on the fluid by the work-energy theorem.
Work is defined as force times distance, and we can separate out the work done in different directions: W = Wx + Wy = Fx1 x1 + Fx2 x2 + Fy1 y1 + Fy2 y2. The following diagram will help, as diagrams do.

There's *gasp* a height difference in these sections of pipe. No need to panic, because potential energy is true for pipes, and we can separate out the horizontal forces from the vertical ones and then add them back together at the end.
Let's start with the x-direction, without a height increase. The fluid under pressure P1 travels through area A1 at a velocity v1 and crosses a distance of x1.
This means the first term of our work equation, Fx1 x1, is given by P1 A1 x1 because force is related to pressure by F = PA. And what is area times length (A1 x1)? Volume V1.
We may simplify the first term to P1V1.
The second term in the x-direction is the same with 2's in it, only we have to remember that force is a vector. Because the fluid goes from having velocity v1 to v2, we determined the fluid accelerates. However, Isaac Newton clearly insisted that an object always resists a change in velocity (the couch potato law), so Fx2 actually opposes this change in velocity. Mathematically, we add a negative sign to Fx2. All together, Wx then equals P1V1 − P2V2.
We can also think about this as negative work .
Sighs of relief and high fives; we've figured out that Wx = P1V1 – P2V2.
What about the y-direction? We turn our attention now to Wy. The only force in this direction is gravity (W = F = -mg). As the fluid rises by a height of the difference of y2 – y1, gravity does negative work such that Wy = -mg (y2 – y1). The fluid has to fight the force of gravity, but that's it.
Our entire equation can then be written as W = P1V1 – P2V2 + mgy1 – mgy2.
Going back to the work-energy theorem, we can fill in some blanks.
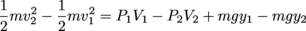
We next isolate the 1's and 2's:
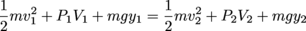
Since m = ρV is in terms of density and volume, we finally, finally get Bernoulli's equation
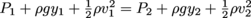 , or
, or 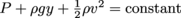 .
.Whew! We did it. Shall we take it for a test drive? Nah. We'll take a break first and practice later.
Believe it or not, Bernoulli's equation lays the foundation of how airplanes function, amongst other things.
Lift, as in air lift, is explained as a difference of pressure. Air molecules have a higher velocity when they fly over the curved side of an airplane wing because of the greater distance: those air molecules have further to go to meet up at the other side with the ones who pass under the straight side of the wing. The pressure of air depends on the velocity of its particles, so the pressure above the wing is less than the pressure below. In essence, the high pressure at the bottom of the wing is what creates lift, which is essential for the flight of airplanes.
The following diagram shows how lift works:

Okay, now we'll try out Bernoulli's equation for ourselves.
A pipe ascends vertically for 8 feet, or 2.3 m. The velocity of the water at both top and bottom of the pipe is
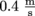 , and as usual the density is
, and as usual the density is 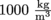 . The pressure at the top is open to the atmosphere because it's coming out of a faucet. What's the pressure at the bottom?
. The pressure at the top is open to the atmosphere because it's coming out of a faucet. What's the pressure at the bottom?Let's look at the equation and see what else we know:
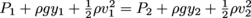 . We're looking for P1, and we know that P2 is atmospheric pressure, which is 1.01 × 105 Pa. We may call y1 zero and y2 = 2.3 m. The velocity terms are identical on both sides of the equation because velocity is constant so they cancel each other out, and we know ρ and g.
. We're looking for P1, and we know that P2 is atmospheric pressure, which is 1.01 × 105 Pa. We may call y1 zero and y2 = 2.3 m. The velocity terms are identical on both sides of the equation because velocity is constant so they cancel each other out, and we know ρ and g. This leads to
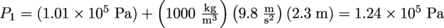 . Gauge pressure, as before, just subtracts atmospheric pressure, or 22,540 Pa. Not that we were asked. We like to go above and beyond the call at duty sometimes, just to shake things up.
. Gauge pressure, as before, just subtracts atmospheric pressure, or 22,540 Pa. Not that we were asked. We like to go above and beyond the call at duty sometimes, just to shake things up.