Mechanics of Fluids
Forces
Before we can talk about fluids, we need to talk about a few other things to help us talk about fluids like forces. Remember what a force is? No, not the Force but a force. We associate force with strength. That actually isn't too far off.In physics, we divide forces into three main categories:
- Electromagnetic
- Nuclear
- Gravitational

Newton's Laws
The guy with or without the fancy wig with the apple is Sir Isaac Newton. He wasn't a "Sir" at the time of the apple, though, but according to legend, one day he was peacefully napping under a tree when an apple fell hitting him on the head. And Boom. An idea struck. From this fictional but popular apple incident, he was not only able to understand gravity, but also develop three laws that explain how things move.Newton's First Law
This law is what some call the law of inertia, or the couch potato law. If we are vegetating on the couch, or sleeping under an apple tree, chances are we won't want to move much. In other words, a body at rest will have a tendency to remain at rest since it's already resting.If an object isn't moving, then the acceleration is zero. Nonexistent. The forces are balanced, so no motion results. If the forces on that object change then their sum, or "net force", causes acceleration in the direction of the net force. But we digress: we're talking inertia.
The law of inertia extends to motion, not just objects at rest. If we're excited about a project, like learning this module for instance, we progress. If we pace ourselves in a way that we learn the same amount of brain-stimulating physics per day, we're learning at a constant rate, or at a constant speed. A constant speed means zero acceleration, too, so in fact we are left with the same scenario: we're not changing pace and we don't want to. This means that a body in motion will have a tendency to remain in motion since it's already moving. This is Newton's First Law.
Newton's First Law states that a body at rest or traveling at constant velocity will remain at rest (or traveling at constant velocity) until it is acted on by a force.
Quantifying Inertia
Sir Isaac Newton translated his laws into math, which is everyone's favorite part because the math is more concise than the words.To understand inertia, all we have to do is understand what a sloth is. Sloths are some of the slowest creatures on Earth. Inertia is pretty much a measure of "slothness."
Although Mom might argue differently, we can't measure how sloth-like we are. But something we can measure, however, is mass. The heavier a sloth is, the more effort it'll have to make to spring off the couch to go get popcorn. That's true of anything in the universe, which tells us that mass is just a quantity of inertia.
Newton's Second Law
Basically, Newton's Second Law states that F = ma. The force applied on an object is simply mass (in kilograms) times the acceleration of the object. Velocity is measured in meters per second (though cars use miles per hour). Acceleration, then, is defined as the change in velocity divided by the difference in time with units of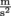 .
.The units of force are found by,
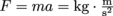 , where
, where  is defined as 1 Newton (N).
is defined as 1 Newton (N).We can calculate more than force with Newton's Second Law, F = ma. For example, a force of 500 N causing an acceleration of
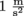 means that the mass of whatever object is accelerating is 500 kg.
means that the mass of whatever object is accelerating is 500 kg.Newton's Third Law
Ever watched an argument between siblings? He did something, she did something, and chances are, whatever she did served him right. Or so she thought. In her revengeful state of mind, she probably tried to at least counter effect what he did to her. If he stole a dollar, then she might've stolen, say, a Snickers bar from him which probably cost around a dollar anyway.This childish fight actually can describe Newton's Third Law: every action has an opposite and equal reaction. If we rest on the couch (refer to the couch potato law), we're exerting a force on the couch because of gravity, but the couch is exerting the exact same force right back on us, in the opposite direction—otherwise, we'd fall right through to the floor.
When we consider our own motion, we don't consider the forces we exert (like on the couch) but the ones on us. When we sit on couches, we have two: the force of gravity and the force from the couch holding us up.
This "couch force" may be called the normal force. In math-and-physics speak, the "normal" direction is perpendicular to the surface on which an object rests, since something on the couch rests parallel to the floor, the "couch force" is perpendicular to it.
Force Diagrams
The fact we're not moving on the couch implies we're in a state of equilibrium. All the forces acting on us add up to zero, or cancel out.We describe forces using vectors and scalars. Vectors describe objects (like forces) with two attributes, a quantity and a direction. We represent vectors with arrows, with the length of the arrow proportional to the quantity of what it represents, be it force, velocity, or momentum. Or something else. A scalar, on the other hand, only defines a number, such as a size. Speed is a scalar quantity, the velocity without direction.
If two forces of the same quantity were applied in the same direction, it doubles the force, but if they oppose each other, then they cancel each other out. Consider the normal force (the couch-force) and gravity shown in the diagram.
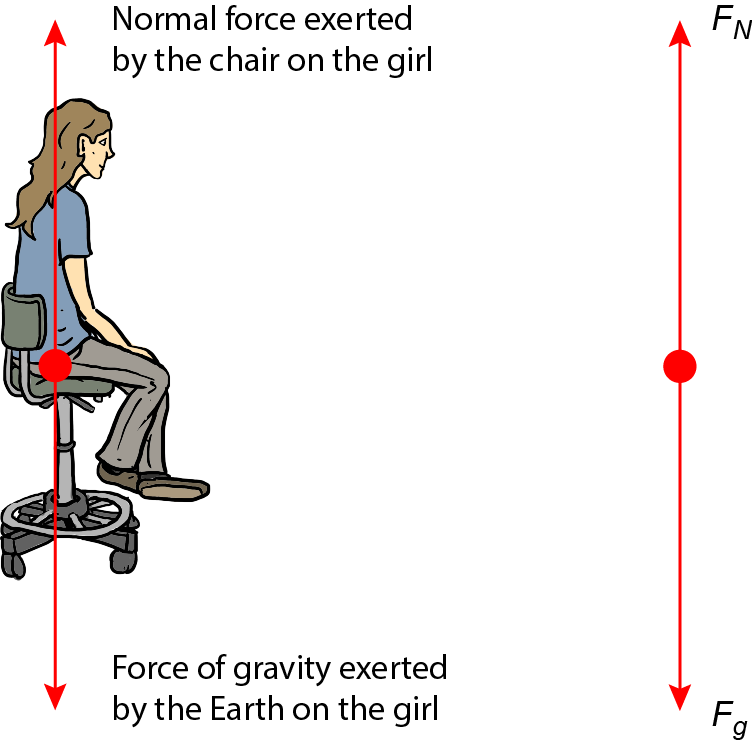
This force diagram illustrates the concept of equilibrium: the force of gravity, mg, is equal in size but opposite in direction to the normal force, N. Force diagrams show all the forces acting on an object, but not the reaction forces that the object itself performs, such as our own gravitational pull on the Earth or push on the couch.
If an object hurtles to the earth in free fall, the only force acting upon it is gravity. Well, air resistance, too, if it isn't negligible. We'd draw that force diagram as the object with a large downward arrow and a tiny upward one, creating a net force downward towards earth, causing acceleration.
We're getting impatient because we really, really want to learn about fluids. Our impatience is about to be gratified.
Forces, Fluids, and Fuji Apples
So what's really going on in fluids? According to everything we've just read, fluids are the norm in the universe since the term applies to all gases and liquids and some solids.We can think of a fluid as a glob of particles, and we know that the state of the fluid is determined by how strongly and tightly the particles in that glob connect to one another. The stronger they connect the more solid the fluid. This glob of particles obeys Newton's three laws just like everything else in the universe.
The particles in a gas bounce around like children with a lot of energy, only rarely interacting with each other. Water molecules in a bottle not only exert forces on each other, but also on the bottle itself, and the bottle pushes right back on the molecules, same thing with an amorphous solid.
Molecules are in continuous motion. Since there are millions of molecules in objects of various sizes, you can see how it would take an eternity to analyze fluid motion one molecule at a time. This is why physicists have come up with much easier ways to deal with fluids.
When we deal with fluids we'll approximate it. That means we'll think of the fluid as being continuous (only one thing) rather than a bunch of separate particles hanging around each other. As long as we understand that the following sections approximate what really happens, we won't have to analyze a drop of water by analyzing the interaction of its 1021 molecules.
By the way, since water is H2O, there are 3 atoms per molecule, which is 3 × 1021 atoms to consider. We'll stop there. We are here to…simplify our lives.
