Hydrostatic Equilibrium
Atmospheric Pressure
Ever heard of atmospheric pressure? When people talk about the weather, they drop information about atmospheric pressure all the time, even if people have no idea what it is. So, what is it?In a manner of speaking, atmospheric pressure is the weight of the atmosphere. Atmospheric pressure depends on the area over which this weight is applied, though—weight and area, sounds like pressure to us.
Let's get something straight: mass is not equal to weight. This is a common misconception in physics. Mass is a measure of the quantity of matter. Weight, on the other hand, is a force. The weight of any object is related to its mass by Newton's Second Law, F = ma. We knew Isaac Newton wasn't going anywhere. To find the pressure
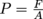 for something where the pressure comes from the force of gravity, we need to know the weight W, which is the force, F. The force of gravity is either Fg or W = mg, where the acceleration of gravity for any object on Earth is g = 9.8
for something where the pressure comes from the force of gravity, we need to know the weight W, which is the force, F. The force of gravity is either Fg or W = mg, where the acceleration of gravity for any object on Earth is g = 9.8 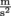 . We might say that
. We might say that 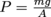 , but what's the mass of all the air?
, but what's the mass of all the air?The weight of the air is difficult to quantify, so scientists get around that by defining pressure instead. Atmospheric pressure is the pressure of the atmosphere at sea level. Naturally, sea level varies since the Earth has a multitude of cliffs, mountains, and forests. Sea level is then always meant as an average. We define 1 atmosphere as the average pressure of the atmosphere at sea level such that 1 atm = 1.013 × 105 Pa.
By measuring pressure relative to atmospheric pressure, we need to define another term, gauge pressure. Gauge pressure is defined as the excess pressure above atmospheric pressure. Absolute pressure is the total pressure.
Depth and Pressure
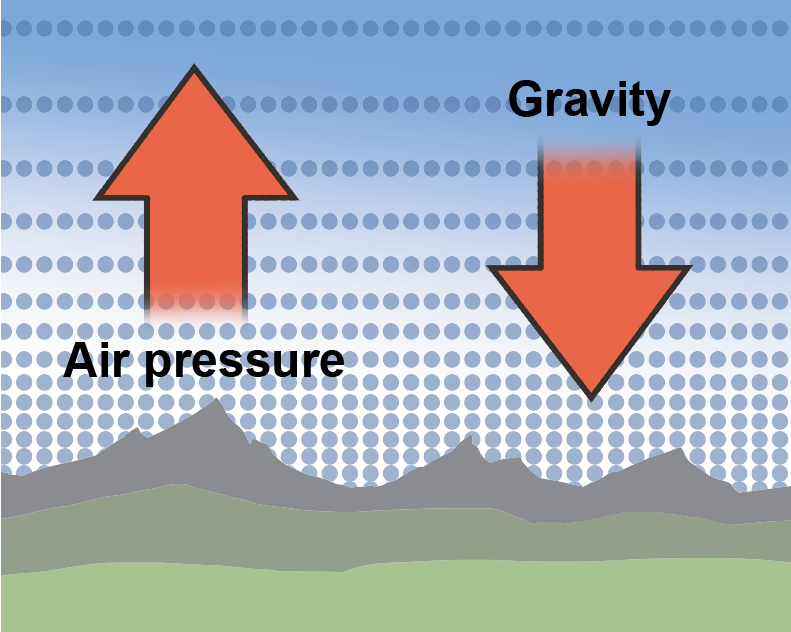
Altitude is the height above sea level, and as altitude increases, atmospheric pressure decreases because there is less air "sitting" on higher altitudes. Air is a fluid, like all gases. Logically then, we would expect that the less fluid there is around us, the less pressure we feel. Hypothesis formed. Let's think about it some more.Take water, for instance. Swimming to the bottom of a pool increases the pressure in our ears. It's because the deeper we swim, the more water weight presses on our bodies. The hypothesis holds.
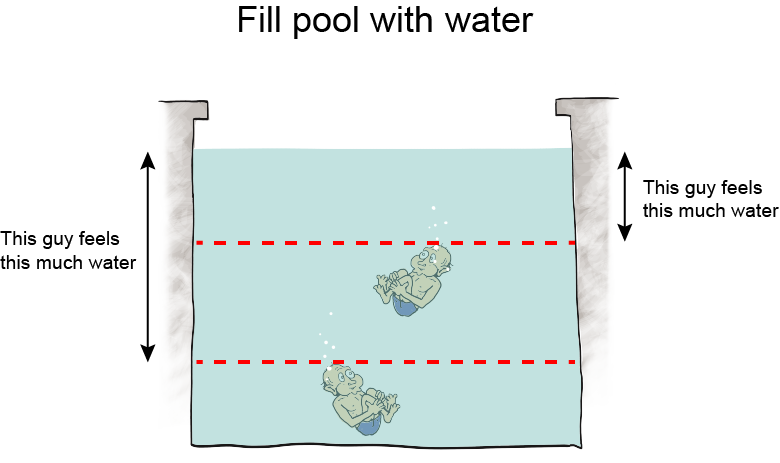
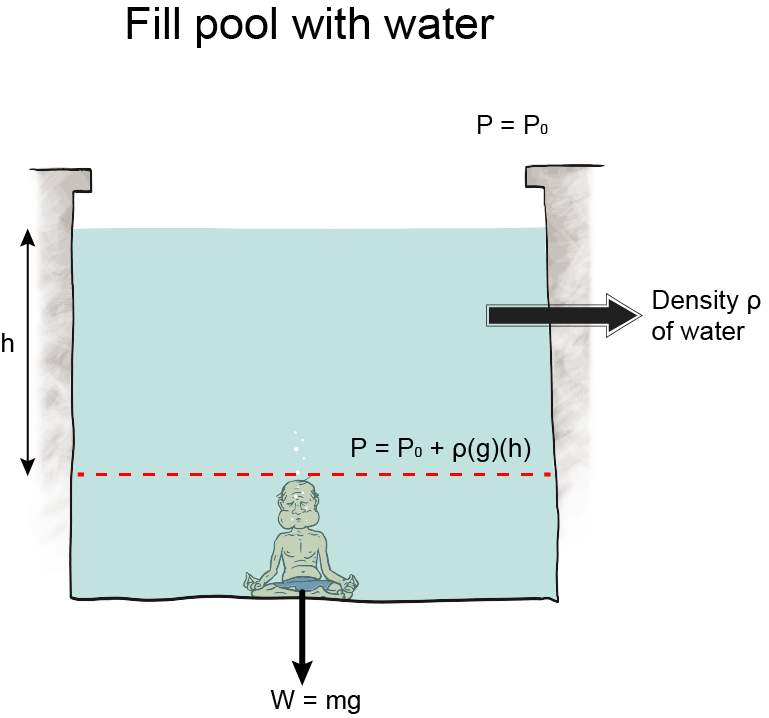
We can still use this equation, though, even though we don't know any calculus. Here it is: P = ρgh. Using this equation, we calculate how much water pressure there is at different depths in any body of water, a swimming pool, the ocean, you name it. We can use the equation to calculate the pressure of any fluid at all, actually, and that makes it pretty nifty.
In P = ρgh, P represents the pressure, ρ is the density of the fluid, and g is the acceleration due to gravity of
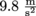 , which is essentially constant anywhere near the surface of the earth. Oh, and h is the height of the fluid pushing down.
, which is essentially constant anywhere near the surface of the earth. Oh, and h is the height of the fluid pushing down.We tweak this equation to find the pressure in different situations. Like underwater, we use P = P0 + ρgh, P represents the pressure at a certain depth, P0 is the initial pressure at the surface, and ρ, g, and h are the same.
In terms of this equation, we can then write another equation for gauge pressure as Pg = P – P0 = ρgh. It's the difference in pressure from atmospheric pressure. Diving down 12 feet (3.66 m) adds
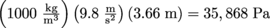 of pressure above atmospheric pressure, which is 1.013 × 105 Pa. We encounter gauge pressure frequently. Every time we operate an instrument that measures pressure, we are in fact measuring pressure relative to atmospheric pressure. This includes barometers and manometers.
of pressure above atmospheric pressure, which is 1.013 × 105 Pa. We encounter gauge pressure frequently. Every time we operate an instrument that measures pressure, we are in fact measuring pressure relative to atmospheric pressure. This includes barometers and manometers.The pressure under water is a gauge pressure too, relative to the atmospheric pressure at the top of the water.
Altitude and Pressure
Can we apply our P = P0 + ρgh equation to other scenarios, such as climbing a mountain? Well, yes and no. Because water isn't as compressible as a gas, its density is more or less constant. That isn't the case for air. The density of air drops as the altitude increases. So let's explore air.First things first. What is air made out of?
Our first instinct may scream, "Oxygen," which is true, but at a lower concentration than we might think. Let's take a look at the diagram below, which breaks down air in percentages of different gases:
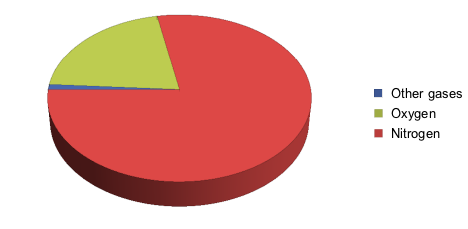
We see that air is actually mostly made up of nitrogen.
Now, that we know what the atmosphere is made out of, we should mention that the atmosphere isn't the same everywhere. Earth's atmosphere feels a gravitational pull just like we do. Gravity helps keep more air nice and tight, close to the surface where we breathe it. That means that hikers aren't just puffing and huffing because they're doing lots of healthy exercise, they're up in the mountains where the air is literally thinner, so it's harder to breathe.
However, just because the atmosphere is less dense once we get to higher altitudes, that doesn't mean its content changes. Air in higher altitudes is still only 20% oxygen, but since there is less air, there is less oxygen too. The following diagram depicts the density of air by height.
Pascal's Law
Let's take a look again at the lovely pressure equation.P = P0 + ρgh
What happens when we multiply P by a constant, say the number 5?
We get (5 × P) =5 × (P0 + ρgh) =5P0 + 5ρgh.
That tells us that if we start with a gas enclosed in a container and compress a part of it to increase its pressure, the pressure at every depth in the container increases by exactly the same amount.
In 1653, that's exactly what a French guy called Blaise Pascal realized. He formulated what is known today as Pascal's Law. If we apply pressure to an enclosed fluid, then every part of the fluid feels the pressure. It looks like all's fair in pressure and fluids.
Monsieur Pascal made the headline news because he specifically said the fluid needed to be enclosed. An enclosed fluid just means the fluid can't escape out of its sealed container. The container can be cylindrical or octopus shaped, it doesn't matter, but it has to be sealed.
If we think about it, applying pressure to a non-enclosed fluid doesn't make much sense. A liquid would pour out and make a mess and gas particles would leave the container, and thus pressure would remain atmospheric.
Now, let's take a step back and think about our original definition of pressure as force divided by area, or
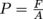 .
.What if the container's shape allows a fluid to occupy different areas at different parts?
As it turns out, because there is more of a fluid in parts with more area (and old Pascal tells us all the fluid will feel the pressure equally), these different areas feel different amounts of force. As long as the applied pressure P (the ratio of force to area) stays constant everywhere, then we aren't breaking any laws of physics.
In other words,
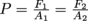 , which is the mathy way of writing Pascal's Law.
, which is the mathy way of writing Pascal's Law.So, where does this bring us? Why, to wonderful things, of course. The diagram below illustrates one of the many useful applications of Pascal's Law: the hydraulic lift, not patented until 1795 by the same British gent, Joseph Bramah, who invented the flush toilet. Blaise Pascal and Joseph Bramah, you have our thanks.
Pascal's Law paved the way (in part) for the industrial revolution. Physics wins again.
Here's an example: If a hydraulic lift puts 5000 N on to 0.04 m2, how much mass could be lifted on the other end if the second area is 2 m2?
Pascal's Law to the rescue. We use
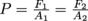 and substitute in
and substitute in 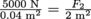 and solve for F2 = 250,000 N. That's the force on the other end, or weight it could lift. To find the corresponding mass, we use Newton's Second Law Fg = mg with the force we just found and
and solve for F2 = 250,000 N. That's the force on the other end, or weight it could lift. To find the corresponding mass, we use Newton's Second Law Fg = mg with the force we just found and 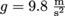 , which means that this hydraulic system could lift a 25,510 kg object. With 2.2 lb in a kilogram, that's 56,122 lbs or 28 tons. This is the hydraulic lift for semitrailers.
, which means that this hydraulic system could lift a 25,510 kg object. With 2.2 lb in a kilogram, that's 56,122 lbs or 28 tons. This is the hydraulic lift for semitrailers. Common Mistakes
Since Pascal's Law involves two ratios, we have to mind our p's and q's, figuratively speaking. Fractions and their values get turned upside down sometimes when numerators and denominators change, just think of versus
versus 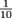 . The first yields 1, but the second is equal to 0.1. A smaller denominator means a larger number.
. The first yields 1, but the second is equal to 0.1. A smaller denominator means a larger number.