Test Your Knowledge
States of Matter
1. While making a carrot cake for her physics professor, Nicole uses the following ingredients: flour, sugar, eggs, milk, raisins, and carrots. After mixing all ingredients, she pours the batter in a heart-shaped pan and preheats the oven to 300 oC. After the cake bakes and cools down, she tops it with extra cream cheese frosting and swirls caramel syrup over it. How many states of matter did the cake occupy while she slaved away in the kitchen?2. Just like water, mercury is liquid at room temperature (around 20 oC – 25 oC). However, mercury boils at around 360 oC and is solid at about -39 oC. How many states of matter can mercury occupy?
3. Just like water, mercury is liquid at room temperature (around 20 oC – 25 oC). However, mercury boils at around 360 oC and is solid at about -39 oC. What phase does it occupy on a 32˚ F day?
4. What is an example of something that is not a fluid?
5. A high (atmospheric) pressure system blows in following a low pressure system, announces the weather forecaster. What words may describe the particles in the system?
1. Answer: The answer is three: solid, liquid, gas. Mixing liquid and solid ingredients, plus heating them up to turn the batter into a solid cake means the liquids evaporated during the baking process.
2. Answer: Is this a trick question? It still has three states of matter. Temperatures of phase changes don't change the number of phases.
3. Answer: The phases changes of mercury are listed in Celsius, so we convert 32 ˚F into 0 ˚C to say definitively that mercury's still a liquid on that day.
4. Answer: A crystalline solid can't flow under any circumstances. It's molecules are locked too rigidly to allow that. This means most metals and rocks and all gems aren't fluids.
5. Answer: The particles are both fluids and gases. Air is a fluid, as are all gases. Betcha hadn't realized we breathe fluids from the moment we're born before.
Mechanics of Fluids
1. With respect to Newton's First Law, why is it so important to wear a seat belt while traveling in a car moving, say at 60 mph?2. Omar's pesky little brother weighs 75 pounds. He is 70 kilograms himself. Who has a tendency to be more of a couch potato (has a higher inertia)?
3. Despite all warnings, Einstein too decides to rest beneath an apple tree. Soon enough, an apple falls on his head, just like happened to Newton. Since he wasn't wearing a fashionable padded wig, the apple hurt. If the acceleration due to gravity is
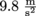 , and the apple weighs 150 grams, how much force does the vicious apple apply on Einstein's poor head?
, and the apple weighs 150 grams, how much force does the vicious apple apply on Einstein's poor head?4. While seeking justice, how much force does Einstein's bruised head apply on the cruel apple?
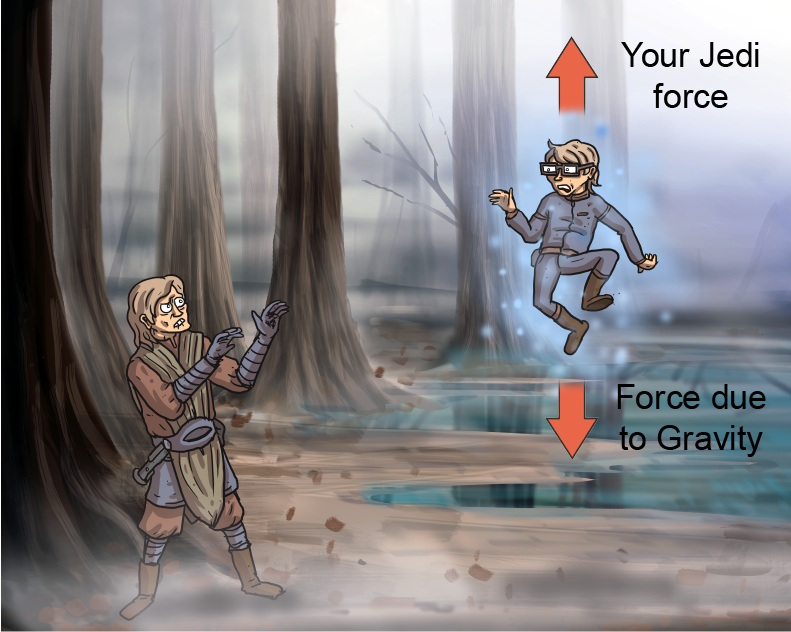
5. While training as a Jedi knight with Master Yoda on his home planet Degobah, Omar's first task consists of making his nameless, pesky little brother levitate off the ground. He weighs 75 lbs on Earth. If the acceleration of gravity on Degobah is half of Earth's, how much Force do you need to use to counteract gravity?
1. Answer: If the car comes to a sudden stop, any body inside it will continue to move at 60 mph until it is acted on by a force. Hopefully, this force comes from a seatbelt and not the windshield.
2. Answer: Mass is proportional to inertia. In this case, Omar resists change in motion more strongly than his brother because of his heavier mass (remember there are 2.2 lb in a kg).
3. Answer: The solution here is to simply apply Newton's Second Law, F = ma. First we convert grams into kilograms with 1 kg = 1000 grams. We can then calculate
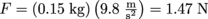 .
.4. Answer: Knowing Newton's Third Law (and the rules of justice), Einstein's head punishes the apple with the exact same amount of force of
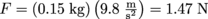 .
.5. Answer: Omar's pesky little brother weight is from the force of gravity, given by F = ma = mg, where g = 9.8 m/s2. He weighs 75 pounds on Earth. Knowing that there is 1 pound in 0.45 kg (the inverse of 2.2 lb per kg), and that half of Earth's acceleration due to gravity is 4.9 m/s2, then on Degobah the necessary force is
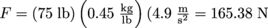 ).
).Density
1. Eris, the Greek goddess of discord, true to her reputation, is roaming about Zeus' fenced garden ready to throw her perfectly spherical apple. If the density of pure gold is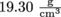 and the apple has a radius of 0.04 m, then what is the apple's mass?
and the apple has a radius of 0.04 m, then what is the apple's mass?2. Eris decides at the last minute that throwing away real gold is stupid, since she could use the gold for herself and perhaps buy friends or something. However, her vindictive nature still pushes her to throw an apple of osmium painted in fake gold over the high fence of Zeus' garden. The density of osmium is
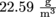 and the apple's size doesn't change. Eris doesn't have the strength to throw an object over 5.5 kg high enough in the air to clear the fence. Does the Trojan War begin?
and the apple's size doesn't change. Eris doesn't have the strength to throw an object over 5.5 kg high enough in the air to clear the fence. Does the Trojan War begin?3. Concerned about the higher density of osmium, Eris decides to mold a smaller apple of osmium. What is the maximum radius of the apple she could make, keeping in mind Eris' strength limit of 5.5 kg to be able to clear the fence?
4. What are the specific gravities of Eris' golden and osmium apples (the one that was too heavy to throw?)
5. What are the specific volumes of these two apples?
1. Answer: By converting the density of gold into
 , we get the very high number of
, we get the very high number of 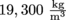 . It's the same density, just in different units. We can assume the apple is a perfect sphere such that its volume is given by
. It's the same density, just in different units. We can assume the apple is a perfect sphere such that its volume is given by  . We plug in the radius of 0.04 m and get a volume of 2.68 × 10-4 m3 for the golden apple.
. We plug in the radius of 0.04 m and get a volume of 2.68 × 10-4 m3 for the golden apple.Next we can use our handy little formula for density and solve for m, such that m = ρV, which returns a mass of 5.17 kg. Eris throws a 5.17 kg apple of gold over the high fence of Zeus' garden? Not bad for a jealous lady.
2. Answer: Just as we did for gold, we convert the density of osmium to standard units of
 . Since the apple's size doesn't change, its volume is still 2.68 × 10-4 m3. Using m = ρV gives us a mass of 6.05 kg. So no, the Trojan war never happened.
. Since the apple's size doesn't change, its volume is still 2.68 × 10-4 m3. Using m = ρV gives us a mass of 6.05 kg. So no, the Trojan war never happened.3. Answer: The maximum mass of the apple has to be 5.5 kg, and the density of osmium is
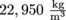 . If we solve for V in the density formula, we get that
. If we solve for V in the density formula, we get that 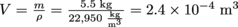 . Since
. Since  , we can next solve for r, which gives a radius of 0.039 m, or 3.9 cm. It's only one millimeter smaller than before.
, we can next solve for r, which gives a radius of 0.039 m, or 3.9 cm. It's only one millimeter smaller than before.4. Answer: Eris' golden apple has a density of
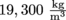 . This means that its specific gravity is
. This means that its specific gravity is 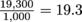 . Her osmium apple has a density of
. Her osmium apple has a density of 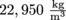 , so its specific gravity is
, so its specific gravity is  .
.5. Answer: If we take the inverse of their densities, we get that
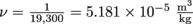 for the golden apple, and
for the golden apple, and 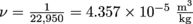 for the apple of osmium. Alternatively we could use
for the apple of osmium. Alternatively we could use 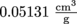 and
and  . They're the same specific densities in different units. Either will do.
. They're the same specific densities in different units. Either will do.Pressure
1. While attending a magic show, a friend volunteers to act as the magician's assistant and lays down on a bed of wood. The bed has a width of 1 m and a height of 2 m. His body has a surface area of 1.8 m2 and mass of 70 kg. How much force is exerted on him by the wood?2. Suddenly, 4000 nails pop out simultaneously from the bed. How much pressure does the nails subject on our dear friend's body?
3. If this same friend lay on a bed of 4000 nails each with a tip area of 1 mm2, then what is the pressure from any one nail?
4. Our 70 kg (foolish) friend next tries to stand up on a single solitary nail with a surface area at the tip of 1 mm2. What's the pressure?
5. If we compress a gas into a smaller volume, does its density increase or decrease?
1. Answer: is the normal force is in equilibrium with the force of gravity. The area measurements are completely irrelevant to this problem. Going back to Newton's Second Law, we use
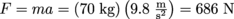
2. Answer: We don't have enough information to solve this one. Instead of the body's surface area, we need the collective area of the tips of the nails, which share the 686 N force from Dear Friend's weight.
3. Answer: The weight (686 N, as we found from #1) is dispersed between 4000 nails, so each nail bears only 0.1715 N. Pressure is force over area, which in standard units is
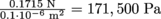 .
.4. Answer: Ooh, bad idea. All 686 N from the force of gravity help up by a single square millimeter? That's a pressure (found only with standard units) of
 .
. 5. Answer: The mass m of the gas doesn't change. Density is always given by
 . If V shrinks down with a constant m, then density increases.
. If V shrinks down with a constant m, then density increases.Hydrostatic Equilibrium
1. We decide to study fluids at the beach. Mom insists we bring her 5-foot wide flowery umbrella to protect us from the sun. Neglecting the umbrella's height, what force does atmospheric pressure apply on the surface of Mom's umbrella?2. After lying under Mom's flowery umbrella at the beach, we decide to move the study session on our new iPad to an air mattress on the water. Suddenly some naked guy drives by on a jet ski shouting "Eureka!" Startled, we drop the iPad into the water and it sinks to the bottom of the ocean (3 meters down). How much pressure is on the iPad at the bottom? The density of salt water is
 .
.3. What is the gauge pressure on the sunk iPad in atmospheres?
4. Show that
 by checking the units in #2.
by checking the units in #2.5. King Hiero's car weighs 1.2 tons and makes a strange noise when it runs. He brings it into a shop run by Mechanic Crook who says he will fix the car based on how much force he needs to apply to his hydraulic lift. The area of the piston is 0.15 m2 and the area of the platform that lifts the car is 30 m2. If Mechanic Crooks charges $10 per unit of force in Newtons, how much will King Hiero pay?
1. Answer: None. The atmosphere is both above and below the umbrella, so it "pressurizes" both sides. If we really want to calculate the amount on just the top or just the bottom though, we'd do it this way. First let's agree to stick to SI units because things will get messy quickly if we don't. One foot = 0.31 m, so the umbrella's width, or diameter, is d = 5 × 0.31 = 1.55 m. This means the umbrella's radius is 0.78 m.
An umbrella is more or less a hemisphere. The surface area of an entire sphere is A = 4πr2, which means that the umbrella's surface area is half of that, or A = 2πr2 = 2π(0.78)2 = 3.82 m2. Atmospheric pressure is 1 atm = 1.013 × 105 Pa, so we solve for F by using F = PA = (1.013 × 105 Pa)(3.82 m2) = 3.87 × 105 N.
2. Answer: The initial pressure Po is simply the atmospheric pressure, 1 atm, which is equal to 1.013 × 105 Pa. Since ocean water is salt mixed in water (right?), the density of salt water should logically be denser than regular water. Our logic is correct. Turns out salt water has a density of around
 , versus
, versus  for regular water.
for regular water.To solve the above problem, we write
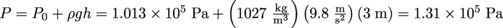 .
.We might say that we're under as much pressure of retrieving it since we'd experience the same 1.31 × 105 Pa of water pressure.
3. Answer: The conversion is 1 Pascal = 9.87 × 10-6 atmospheres, so 1.31 × 105 Pa of pressure is equivalent to 1.29 atm, and Pg = P - Po = 1.29 – 1 = 0.29 atm.
4. Answer: Essentially we need to analyze the units of ρgh, since by definition, Po is already in units of pressure. The units of ρgh are
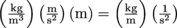 .
.Remembering that
 , we get that
, we get that 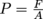 since force is measured in Newtons and multiplying Newtons by area gives us
since force is measured in Newtons and multiplying Newtons by area gives us  .
.As if two units for pressure of Pascals and atmospheres weren't enough, there is another unit. It's the bar and related to atmospheres as 1 atm = 1.013 bar. Incidentally, this is also equal to
 .
.5. Answer: Pascal's Law states that
 . Essentially, we need to know F1 to calculate the cost from it. The force F2 is the weight of the car given by
. Essentially, we need to know F1 to calculate the cost from it. The force F2 is the weight of the car given by 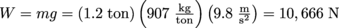 . Then we solve
. Then we solve 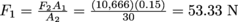 .
.To calculate the cost, multiply the force in Newtons by $10 and Mechanic Crook charges King Hiero $533.30. This would never do for an oil change.
Archimedes' Principle
1. Two of Eris' spherical apples of gold, one with a radius of r1 = 0.04 m, and another with a radius r2 = 0.05 m, are dropped in two separate containers of water. Which apple displaces more water?2. Eris makes a spelling mistake while inscribing her apple (r = 0.05 m) with the words TO THE MOST BEAUTIFUL and melts the gold to start all over again. However, in her rage, she uses the wrong mold. The apple turns out in the shape of prism. Would the prism or the apple displace more water?
3. Eris makes two apples with r = 0.05 m of gold (
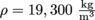 ) and osmium (
) and osmium ( ). Which apple displaces more water?
). Which apple displaces more water?4. The density of salt water is
 . A vicious shark approaches an innocent-looking blowfish that instantly swells up trembling in fear to an approximate sphere of diameter d = 1 m. How much ocean does the blowfish displace when inflated?
. A vicious shark approaches an innocent-looking blowfish that instantly swells up trembling in fear to an approximate sphere of diameter d = 1 m. How much ocean does the blowfish displace when inflated?5. This particular blowfish with a 1 m inflated diameter weighs 22 lb. What is the mass of water taken in by the blowfish in inflating? Use the density of saltwater of
 for both fish and water.
for both fish and water.1. Answer: If these were normal apples, we wouldn't have enough information because they float, and displace less water than the apple's volume. Phew! Dodged that one. The volume of a sphere is proportional to the cube of the radius,
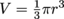 , so the larger radius corresponds to a larger volume of displaced water.
, so the larger radius corresponds to a larger volume of displaced water.2. Answer: The prism and apple have the same volume, regardless of the shape. Therefore, they displace the same amount of water.
3. Answer: If the two apples have the same radius, their volume is the same. The densities are both greater than the density of water (
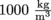 ), so they both sink and each displaces its volume in water. Therefore, they displace the same amount of water.
), so they both sink and each displaces its volume in water. Therefore, they displace the same amount of water.4. Answer: A diameter of 1 m implies a radius r = 0.5 m. The volume of the blowfish is therefore
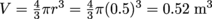 . The blowfish doesn't floats when inflating (or sink: density remains constant at the density of salt water), so the volume of displaced water is the same. The increase in size comes from water intake into special places within the fish, so in a way the blowfish isn't displacing water so much as putting it somewhere else.
. The blowfish doesn't floats when inflating (or sink: density remains constant at the density of salt water), so the volume of displaced water is the same. The increase in size comes from water intake into special places within the fish, so in a way the blowfish isn't displacing water so much as putting it somewhere else. 5. Answer: We can use density to get to mass and then subtract the mass of the fish to find the mass of water alone. Volume is 0.52 m3 as found in #4. Then total mass is volume times density, 534 kg. Here's where we subtract the mass of the fish after converting 22 lb = 10 kg, and therefore the water intake is an astounding 524 kg.
Fluid Dynamics
1. Using the concepts we've learned thus far, would a fluid with a higher density have a higher or lower viscosity, generally speaking?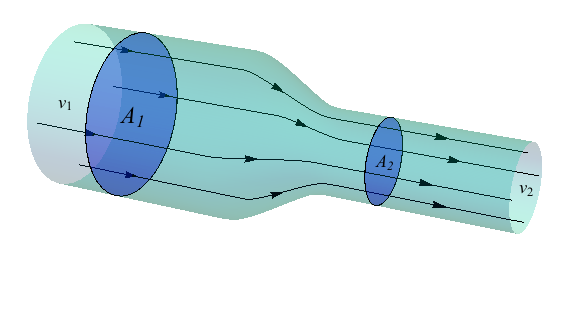
2. In the above diagram, is v2 higher or lower than v1?
3. Professor Higgins devises a new cruel way to teach Eliza Doolittle how to properly enunciate her words. He puts her under an open-ended pipe formed with two different areas, A1 = 20 cm2 and A2 = 10 cm2 such that Eliza stands right underneath A2. Eliza must repeat "The fluid in a flow tube stays always in the flow tube" correctly, else Professor Higgins will turn on the tap and Eliza will get soaked to the bone. Water flows through A1 at a rate of
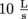 . At what flow rate does water come gushing out of A2 and land on Eliza when she mispronounces her sentence?
. At what flow rate does water come gushing out of A2 and land on Eliza when she mispronounces her sentence?4. In the above problem, at what velocity does water hit Eliza's head?
5. Interpret Bernoulli's equation by examining the units of each term.
1. Answer: A fluid with a high density has more particles packed in a smaller volume. Since there are more particles, there's more internal friction between them. An exception to the rule is mercury, with a high density but relatively low viscosity.
2. Answer: Since A1v1 = A2v2, the larger cross sectional area corresponds to smaller speeds. The speed is larger through a narrow tube so v1 is lower than v2 .
3. Answer: The flow rate
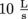 is constant. Water is considered incompressible and has a constant density so we may treat it as an ideal fluid, and its volume flow rate is the same in all areas of the pipe.
is constant. Water is considered incompressible and has a constant density so we may treat it as an ideal fluid, and its volume flow rate is the same in all areas of the pipe.4. Answer: We only have to apply our formula for volume flow rate (with compatible units) to see that v2 is the flow rate over
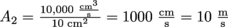 . That's seriously fast flow.
. That's seriously fast flow.5. Answer: If we started with P, we'd probably confuse ourselves. Pascals, atmospheres, bars…The list goes on. So let's first look at
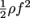 , which incidentally resembles the term for kinetic energy,
, which incidentally resembles the term for kinetic energy, 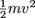 .
.In Bernoulli's equation we have density instead of mass. Density is mass per volume. So this term is actually energy per unit volume, or energy density.
The term ρgy resembles potential energy, mgy, so it also has units of energy density.
And what about P? Pressure is
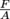 . Multiply both F and A by a unit of length and we are left with work divided by volume, or once again, energy density.
. Multiply both F and A by a unit of length and we are left with work divided by volume, or once again, energy density.Bernoulli's equation shows that energy density is conserved as a fluid moves through a tube, or is an example of the conservation law of energy.