Force of Gravity and Orbital Motion
The force of gravity, famous for allegedly dropping an apple on Sir Isaac Newton’s head and thereby furthering the development of physics, is still perhaps the least understood of standard non-contact forces, which also include electricity and magnetism.
We blame gravity for all behavior on the cosmic scale. Gravity defines the orbits of planets and asteroids and stars, it determines the rate of expansion of the whole universe, too. It poses some of the most exciting questions scientists face today. So, we could say it’s kind of a big deal.
Before we’re prepared to understand the questions about gravity facing scientists today, let’s start with the basics.
Although people sometimes use “weight” and “mass” to mean the same thing, this is not the case. Mass, as we saw earlier, is an intrinsic property of all objects. Weight, on the other hand, is the force corresponding to a particular gravitational field, the size of which is dependent on both mass of the object and the acceleration due to gravity in that field. Mass is characteristic, and weight is a measurement of that characteristic under certain conditions.
This acceleration due to gravity is now known as g, which is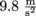 . Any object near the surface of the Earth experience’s this same acceleration, because we’re about the same distance away from the center of the Earth at its surface, so we experience the same gravitational pull.
. Any object near the surface of the Earth experience’s this same acceleration, because we’re about the same distance away from the center of the Earth at its surface, so we experience the same gravitational pull.
It’s Isaac Newton that incorporated Galileo’s findings on the acceleration of gravity. He found the size of force of gravity on a particular object with mass m: it’s Fg = mg. It always points to the center of the Earth. If we’re calling down negative in our frame of reference, then we use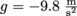 and get a negative force. It’s the force we commonly term “weight.” Sometimes we use W for the force of gravity instead of Fg, but it’s the same thing.
and get a negative force. It’s the force we commonly term “weight.” Sometimes we use W for the force of gravity instead of Fg, but it’s the same thing.
Since the acceleration due to gravity changes with the gravitational body, we weigh less on the moon and more on Jupiter. Our mass is constant anywhere, however. It’s the force of gravity which changes.
Anyone wants to know his or her weight on Mars?
The gravitational acceleration on Mars is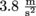 . Approximating that the average high school student is 60 kg, the force of gravity on Mars is
. Approximating that the average high school student is 60 kg, the force of gravity on Mars is 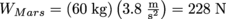 .
.
Without knowing how much 60 kg weighs on Earth, we have no grounds for comparison. On Earth, the weight of 60 kg is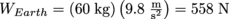 .
.
Since we’re more familiar with weight in pounds than kilograms, we can use the Earth-bound conversion of 1 kg in 2.2 lb to say that this same 60 kg person weighs 132 pounds on Earth, but this conversion doesn’t work for Mars: pounds aren’t the same over there.
Sir Isaac Newton found that celestial bodies, such as our Moon and Earth, are pulled toward all other celestial bodies. The force responsible for this weakens as the square of the distance that separates the interacting masses, what’s known as an “inverse square law.” The two forces are equal to each other because they are an action-reaction pair from Newton’s Third Law of Motion.
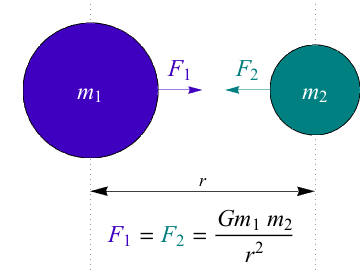
Newton wrote this attractive force as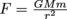 , where M and m are the masses of the two objects, r is the distance between them, and G is the universal gravitational constant equal to
, where M and m are the masses of the two objects, r is the distance between them, and G is the universal gravitational constant equal to 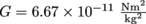 . This constant had to be inserted in order for the forces to correspond to the observed measurements of planetary motions.
. This constant had to be inserted in order for the forces to correspond to the observed measurements of planetary motions.
In essence, what Newton realized was true genius: the force that made the apple fall on the ground was the same force pulling on the Moon while orbiting the Earth!
To recap: the force between two bodies is felt as attractive by each of them, and of the same magnitude. In other words, each action has an equal and opposite reaction—it’s Newton’s Third Law as it applies to gravity. The force of gravity on the Earth from the Moon is the same, though opposite in direction, to the force of gravity on the Moon from the Earth. Newton’s Third Law bears repeating. And repeating. And repeating. Until we're out of bears.
Let’s try an example. The average distance between the Moon and the Earth is 384,400 km. The mass M of the Earth is 5.97 × 1024 kg and the mass of the Moon is 7.34 × 1022 kg. What gravitational pull does each body exert on the other?
Here we have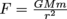 with both M and m given, as well as r which needs to be converted into meters to work with the gravitational constant. Once we plug in the numbers, we find that F = 1.98 × 1020 N.
with both M and m given, as well as r which needs to be converted into meters to work with the gravitational constant. Once we plug in the numbers, we find that F = 1.98 × 1020 N.
How does this formula compare to our simple F = ma? Let’s figure that out.
Our mission, should we choose to accept it, is to reconcile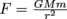 and F = ma. In the first expression, we are dealing with two objects of two masses, M and m separated by a distance r. If we take M to be the mass of Earth, and m to be our mass, then we should in theory pluck out
and F = ma. In the first expression, we are dealing with two objects of two masses, M and m separated by a distance r. If we take M to be the mass of Earth, and m to be our mass, then we should in theory pluck out 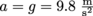 .
.
We then have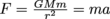 , which results in
, which results in 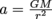 because m cancels out. Since we stand on the surface of the Earth, and its gravity center is, well, at the center, then r is simply the radius of the Earth, r = 6.37 × 106 m. After plugging everything in, we get
because m cancels out. Since we stand on the surface of the Earth, and its gravity center is, well, at the center, then r is simply the radius of the Earth, r = 6.37 × 106 m. After plugging everything in, we get 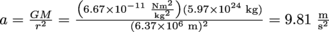 .
.
A ‘planet’s acceleration due to gravity is proportional to its mass and inversely proportional to its radius squared. If we want to find the acceleration at the surface of the planet or moon or whatever, we use the radius of the body itself to calculate that acceleration.
Since the radius of the Earth is so large compared to our height, we don’t have to worry about taking how tall we are into account. Even the tallest mountains on Earth are “only” 7,200 m high. That’s still three orders of magnitude lower than Earth’s radius, and won’t substantially affect any of our calculations.
The answer lies in circular motion. Imagine throwing a ball, or shooting a cannonball (or satellite) so fast that as it drops downward towards the center of the earth, its path curves such that it can never get there, like this. This velocity changes based on the planet or moon or whatever’s orbited.
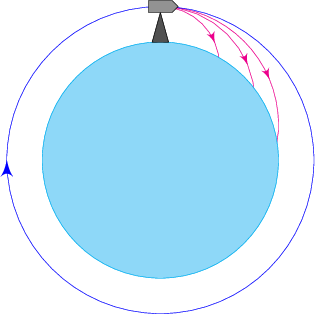
The technical name for a force pointing in towards the center of a circle is centripetal acceleration. The motion resulting from Centripital acceleration is circular motion. Merry-go-rounds, Tilt-a-Whirls, sling shots, curved loops of roller coasters, clover-leaf free-way exits…circular motion is all around us.. Get it? Around? Ahem.
Moving in a circle has more to do with angles than distances, setting circular motion problems apart from the examples of free falls and projectile motion we saw earlier. If we could cut the circle’s circumference and straighten it out flat, the dynamics would appear as linear motion with constant speed.
So where’s acceleration in all this? To answer that question, we need to think about what makes an object keep moving in a circle. To remain on a circular path, the object needs to be constantly changing direction, which means that the object doesn’t have constant velocity and therefore must have a force and acceleration acting on it from Newton’s first and second laws of motion.
Not only that, but the change in direction must be the same from one instant to the next meaning the acceleration and force are constant to keep the speed constant.
At any one instant, we could draw a diagram like the one below. It’s a kind of force diagram too, but with only one force on it, which is a centripetal force.
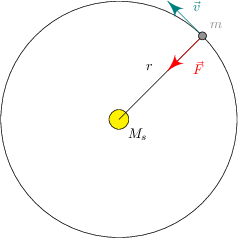
Velocity, acceleration, and force are vector quantities. In centripetal motion, the velocity is tangential to the orbit, and perpendicular to the force and acceleration which are in the same direction, as usual, as related through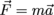 .
.
How do we relate this centripetal acceleration to the speed or velocity? Our former equation of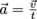 hardly seems to fit the bill as it stands. We need a bit of geometry.
hardly seems to fit the bill as it stands. We need a bit of geometry.
We’ve all heard that a circle has 360 degrees. Degrees aren’t the most convenient unit to work with when we study things going around in a circle, though, radians are. Instead, let’s use the radian-based formula for the circumference of a circle, C = 2πr. Recall that a circle has 2π radians. Everyone loves pi, especially à la mode.
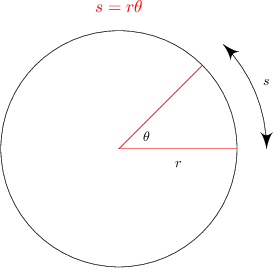
In radian mode, we can multiply the angle by the length of the circle’s radius to obtain the length s of the arc corresponding to that angle, s = rθ. Check this out:
Since velocity times time equals distance even when moving in a circular path, s = vt. We’re using s as the distance and v as the speed. Combining this expression with our previous one of s = rθ, we get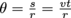 .
.
Using the fact that one full revolution covers the entire circumference C = 2πr, and recalling that the orbital period T is the time an object requires to complete one full revolution, we can write the orbital speed of the object as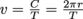 . Angles are swept out over times that are proportionate to the period. In other words, we can write the following relationship:
. Angles are swept out over times that are proportionate to the period. In other words, we can write the following relationship: 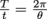 . From there, we can solve for theta,
. From there, we can solve for theta, 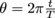 . Remember, angular motion’s θ is like linear motion’s x.
. Remember, angular motion’s θ is like linear motion’s x.
Acceleration equals a change in velocity over time,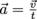 . Here, the veolicty v is constant but the angle θ is constantly changing over a period of time t such that Δv = θv. Then acceleration becomes
. Here, the veolicty v is constant but the angle θ is constantly changing over a period of time t such that Δv = θv. Then acceleration becomes 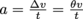 . Remembering that
. Remembering that 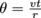 , we substitute this relationship into our expression for a to define the centripetal acceleration as
, we substitute this relationship into our expression for a to define the centripetal acceleration as 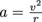 .
.
Ta-daaa!
There’s more: now that we’ve related velocity to acceleration in orbital motion, force becomes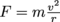 .
.
Then, since the universal law of gravitation is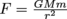 , we can set that equal to
, we can set that equal to 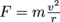 to find the speed required to orbit the larger mass M. Ingenious!
to find the speed required to orbit the larger mass M. Ingenious!
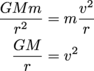
And what’s the orbital velocity required for orbiting planet Earth? To answer that, we have to choose a distance from earth for the orbit. The closer the distance between the two, the faster the necessary velocity to stay in orbit. This is precisely why inner planets have shorter “years” around the Sun than the outer planets. Nor can the velocity change for a given radius: by changing the velocity, the radius of orbit changes too.
We blame gravity for all behavior on the cosmic scale. Gravity defines the orbits of planets and asteroids and stars, it determines the rate of expansion of the whole universe, too. It poses some of the most exciting questions scientists face today. So, we could say it’s kind of a big deal.
Before we’re prepared to understand the questions about gravity facing scientists today, let’s start with the basics.
Weight and the Acceleration of Gravity
Gravity is a force that objects exert on each other based on mass and distance, through a mass-sensitive field. We’re probably most familiar with weight, which is the force that Earth extends on our bodies and on all other massive objects.Although people sometimes use “weight” and “mass” to mean the same thing, this is not the case. Mass, as we saw earlier, is an intrinsic property of all objects. Weight, on the other hand, is the force corresponding to a particular gravitational field, the size of which is dependent on both mass of the object and the acceleration due to gravity in that field. Mass is characteristic, and weight is a measurement of that characteristic under certain conditions.
This acceleration due to gravity is now known as g, which is
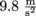 . Any object near the surface of the Earth experience’s this same acceleration, because we’re about the same distance away from the center of the Earth at its surface, so we experience the same gravitational pull.
. Any object near the surface of the Earth experience’s this same acceleration, because we’re about the same distance away from the center of the Earth at its surface, so we experience the same gravitational pull.It’s Isaac Newton that incorporated Galileo’s findings on the acceleration of gravity. He found the size of force of gravity on a particular object with mass m: it’s Fg = mg. It always points to the center of the Earth. If we’re calling down negative in our frame of reference, then we use
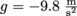 and get a negative force. It’s the force we commonly term “weight.” Sometimes we use W for the force of gravity instead of Fg, but it’s the same thing.
and get a negative force. It’s the force we commonly term “weight.” Sometimes we use W for the force of gravity instead of Fg, but it’s the same thing.Since the acceleration due to gravity changes with the gravitational body, we weigh less on the moon and more on Jupiter. Our mass is constant anywhere, however. It’s the force of gravity which changes.
Anyone wants to know his or her weight on Mars?
The gravitational acceleration on Mars is
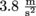 . Approximating that the average high school student is 60 kg, the force of gravity on Mars is
. Approximating that the average high school student is 60 kg, the force of gravity on Mars is 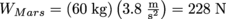 .
.Without knowing how much 60 kg weighs on Earth, we have no grounds for comparison. On Earth, the weight of 60 kg is
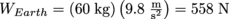 .
.Since we’re more familiar with weight in pounds than kilograms, we can use the Earth-bound conversion of 1 kg in 2.2 lb to say that this same 60 kg person weighs 132 pounds on Earth, but this conversion doesn’t work for Mars: pounds aren’t the same over there.
The Universal Law of Gravitation
Kepler’s study of planetary orbits fascinated Newton. For example, the Earth orbits the Sun because of the Sun’s strong gravitational pull. This is called orbital motion; the sun's gravity makes the Earth stay in orbit around the sun rather than flying out into cold, lonely space.Sir Isaac Newton found that celestial bodies, such as our Moon and Earth, are pulled toward all other celestial bodies. The force responsible for this weakens as the square of the distance that separates the interacting masses, what’s known as an “inverse square law.” The two forces are equal to each other because they are an action-reaction pair from Newton’s Third Law of Motion.

Newton wrote this attractive force as
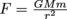 , where M and m are the masses of the two objects, r is the distance between them, and G is the universal gravitational constant equal to
, where M and m are the masses of the two objects, r is the distance between them, and G is the universal gravitational constant equal to 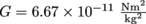 . This constant had to be inserted in order for the forces to correspond to the observed measurements of planetary motions.
. This constant had to be inserted in order for the forces to correspond to the observed measurements of planetary motions. In essence, what Newton realized was true genius: the force that made the apple fall on the ground was the same force pulling on the Moon while orbiting the Earth!
To recap: the force between two bodies is felt as attractive by each of them, and of the same magnitude. In other words, each action has an equal and opposite reaction—it’s Newton’s Third Law as it applies to gravity. The force of gravity on the Earth from the Moon is the same, though opposite in direction, to the force of gravity on the Moon from the Earth. Newton’s Third Law bears repeating. And repeating. And repeating. Until we're out of bears.
Let’s try an example. The average distance between the Moon and the Earth is 384,400 km. The mass M of the Earth is 5.97 × 1024 kg and the mass of the Moon is 7.34 × 1022 kg. What gravitational pull does each body exert on the other?
Here we have
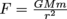 with both M and m given, as well as r which needs to be converted into meters to work with the gravitational constant. Once we plug in the numbers, we find that F = 1.98 × 1020 N.
with both M and m given, as well as r which needs to be converted into meters to work with the gravitational constant. Once we plug in the numbers, we find that F = 1.98 × 1020 N.How does this formula compare to our simple F = ma? Let’s figure that out.
Our mission, should we choose to accept it, is to reconcile
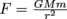 and F = ma. In the first expression, we are dealing with two objects of two masses, M and m separated by a distance r. If we take M to be the mass of Earth, and m to be our mass, then we should in theory pluck out
and F = ma. In the first expression, we are dealing with two objects of two masses, M and m separated by a distance r. If we take M to be the mass of Earth, and m to be our mass, then we should in theory pluck out 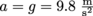 .
.We then have
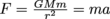 , which results in
, which results in 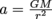 because m cancels out. Since we stand on the surface of the Earth, and its gravity center is, well, at the center, then r is simply the radius of the Earth, r = 6.37 × 106 m. After plugging everything in, we get
because m cancels out. Since we stand on the surface of the Earth, and its gravity center is, well, at the center, then r is simply the radius of the Earth, r = 6.37 × 106 m. After plugging everything in, we get 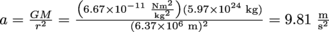 .
.A ‘planet’s acceleration due to gravity is proportional to its mass and inversely proportional to its radius squared. If we want to find the acceleration at the surface of the planet or moon or whatever, we use the radius of the body itself to calculate that acceleration.
Since the radius of the Earth is so large compared to our height, we don’t have to worry about taking how tall we are into account. Even the tallest mountains on Earth are “only” 7,200 m high. That’s still three orders of magnitude lower than Earth’s radius, and won’t substantially affect any of our calculations.
Orbital Motion
If any two massive bodies gravitationally attracted to each other, why don’t they accelerate towards, and crash into each other? Sometimes this does happen, but not most of the time. The Moon isn’t in danger of falling to Earth, for example. Or the Earth falling into the Sun. Why not?The answer lies in circular motion. Imagine throwing a ball, or shooting a cannonball (or satellite) so fast that as it drops downward towards the center of the earth, its path curves such that it can never get there, like this. This velocity changes based on the planet or moon or whatever’s orbited.

The technical name for a force pointing in towards the center of a circle is centripetal acceleration. The motion resulting from Centripital acceleration is circular motion. Merry-go-rounds, Tilt-a-Whirls, sling shots, curved loops of roller coasters, clover-leaf free-way exits…circular motion is all around us.. Get it? Around? Ahem.
Moving in a circle has more to do with angles than distances, setting circular motion problems apart from the examples of free falls and projectile motion we saw earlier. If we could cut the circle’s circumference and straighten it out flat, the dynamics would appear as linear motion with constant speed.
So where’s acceleration in all this? To answer that question, we need to think about what makes an object keep moving in a circle. To remain on a circular path, the object needs to be constantly changing direction, which means that the object doesn’t have constant velocity and therefore must have a force and acceleration acting on it from Newton’s first and second laws of motion.
Not only that, but the change in direction must be the same from one instant to the next meaning the acceleration and force are constant to keep the speed constant.
At any one instant, we could draw a diagram like the one below. It’s a kind of force diagram too, but with only one force on it, which is a centripetal force.

Velocity, acceleration, and force are vector quantities. In centripetal motion, the velocity is tangential to the orbit, and perpendicular to the force and acceleration which are in the same direction, as usual, as related through
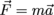 .
. How do we relate this centripetal acceleration to the speed or velocity? Our former equation of
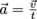 hardly seems to fit the bill as it stands. We need a bit of geometry.
hardly seems to fit the bill as it stands. We need a bit of geometry. We’ve all heard that a circle has 360 degrees. Degrees aren’t the most convenient unit to work with when we study things going around in a circle, though, radians are. Instead, let’s use the radian-based formula for the circumference of a circle, C = 2πr. Recall that a circle has 2π radians. Everyone loves pi, especially à la mode.
In radian mode, we can multiply the angle by the length of the circle’s radius to obtain the length s of the arc corresponding to that angle, s = rθ. Check this out:

Since velocity times time equals distance even when moving in a circular path, s = vt. We’re using s as the distance and v as the speed. Combining this expression with our previous one of s = rθ, we get
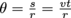 .
.Using the fact that one full revolution covers the entire circumference C = 2πr, and recalling that the orbital period T is the time an object requires to complete one full revolution, we can write the orbital speed of the object as
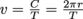 . Angles are swept out over times that are proportionate to the period. In other words, we can write the following relationship:
. Angles are swept out over times that are proportionate to the period. In other words, we can write the following relationship: 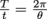 . From there, we can solve for theta,
. From there, we can solve for theta, 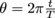 . Remember, angular motion’s θ is like linear motion’s x.
. Remember, angular motion’s θ is like linear motion’s x.Acceleration equals a change in velocity over time,
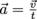 . Here, the veolicty v is constant but the angle θ is constantly changing over a period of time t such that Δv = θv. Then acceleration becomes
. Here, the veolicty v is constant but the angle θ is constantly changing over a period of time t such that Δv = θv. Then acceleration becomes 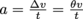 . Remembering that
. Remembering that 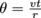 , we substitute this relationship into our expression for a to define the centripetal acceleration as
, we substitute this relationship into our expression for a to define the centripetal acceleration as 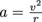 .
.Ta-daaa!
There’s more: now that we’ve related velocity to acceleration in orbital motion, force becomes
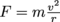 .
.Then, since the universal law of gravitation is
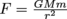 , we can set that equal to
, we can set that equal to 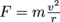 to find the speed required to orbit the larger mass M. Ingenious!
to find the speed required to orbit the larger mass M. Ingenious! 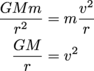
And what’s the orbital velocity required for orbiting planet Earth? To answer that, we have to choose a distance from earth for the orbit. The closer the distance between the two, the faster the necessary velocity to stay in orbit. This is precisely why inner planets have shorter “years” around the Sun than the outer planets. Nor can the velocity change for a given radius: by changing the velocity, the radius of orbit changes too.