Rotation and Energy
To complete the tools you need to analyze rotational motion, we need one more concept from translational kinematics: energy. Rotating objects can still have kinetic and potential energy, but spinning adds a new type of mechanical energy to our collection: rotational kinetic energy.
Like all forms of mechanical energy, rotational kinetic energy obeys the Law of Conservation of Energy. This means that, like the One Ring, it cannot be created or destroyed save for in the mighty fires of Mount Doom itself. We are, however, free to change rotational kinetic energy into other forms of mechanical energy as we so desire. (A catapult, for example, turns the rotational motion of the weapon's arm into translational motion of the projectile.)
Just like objects can have both kinetic and potential energy, nothing is preventing an object from having both translational kinetic energy and rotational kinetic energy. In fact, this is something pretty common—it's a form of motion called rolling.
What physicists call "rolling" happens when an object is rotating and moving translationally: think car tires, bicycles, bowling balls. You hit the gas pedal, push on the bike pedals, or hurl the bowling ball down the lane, and all three objects move translationally—but also spin around their central axis. You see them rollin', you best not be hatin'.
The total mechanical energy of a rolling object is equal to the sum of its translational kinetic energy (based on its translational speed v) and its rotational kinetic energy (based on its rotational speed ω), plus any potential energy it might have. This is different than objects that only spin—tops, hula hoops, gyroscopes—which will only have rotational kinetic energy, and objects that only slide, such as blocks on frictionless tables, which will only have translational kinetic energy. Rolling motion is the combination of the two.
Translational kinetic energy is given by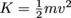 . Rotational kinetic energy, continuing our analogy quite nicely, is:
. Rotational kinetic energy, continuing our analogy quite nicely, is:

Energy is energy, though, and this is still measured in joules—check for yourself.
This means the total kinetic energy of any object is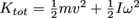 . For spinning objects, v = 0; for sliding objects, ω = 0. For rolling objects, neither v nor ω are zero.
. For spinning objects, v = 0; for sliding objects, ω = 0. For rolling objects, neither v nor ω are zero.
Rotational Work
The concept of work in physics, recall, is blue collar in the extreme: forces show up, clock in, act continuously over a distance, then clock out and head home to their family. Work is a measure of an object's change in energy when a force acts on it—it is work that captures, for example, the change in kinetic energy of an accelerating car, based on the force exerted by the engine.
But what about the tires of the car? There is some work done speeding them from zero rpms to hundreds of rpms as the car accelerates, because the rotational kinetic energy of the tires changes. This change in rotational energy is called, appropriately enough, rotational work. Just as translational work is done by a force acting over a distance (W = Fd), rotational work is done by a torque acting over an angle:
Wrot = τθ
Since rotational work measures the change of rotational kinetic energy of an object as it is spun by some torque, there is also a work-energy theorem for rotational motion:
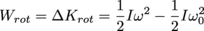
Here ω is an object's final angular velocity and ω0 is its starting angular velocity.
Rotational work and translational work are both measures of energy change, and so are both measured in joules.*
Rotational Power
If work can be extended to rotational motion as rotational work, then power—the rate at which an object can do work—must also have a rotational analog: rotational power.
While the basic definition is the same (power is power, and will always measure the rate at which an object can do work), we can calculate an object's power output by measuring its torque output. This is similar to translational motion, where an object's power is given by the force it can output multiplied by the speed it moves whatever that force acts on (P = Fv). Rotationally, the power of an object can be found by multiplying the torque it can output and the angular speed it moves whatever that torque acts on:
Prot = τω
But the two definitions of power measure the same thing. Imagine a winch, a device with ropes and pulleys used to hoist heavy objects.

Winch engines are often rated in horsepower, the same way car engines are. This is a measure of how fast the winch can do work—or, equivalently and more concretely, how fast the winch can lift things. A 2 hp (1492 W) engine can lift a 100 kg box at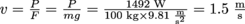 .
.
If the pulley on the winch has a 10 cm radius, then to move that same 100 kg weight, it must turn a torque of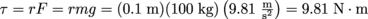 . It can turn this torque at a rate of
. It can turn this torque at a rate of 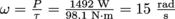 .
.
15 rad/s on a pulley with a 0.1 m radius is equivalent to a tangential velocity of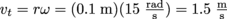 .
.
Boom.
Common Mistakes
Rotational energy, work, and power are all convertible to their translational equivalents, and are measured in the same units. This is very different than angular velocity, acceleration, and momentum, which are all only analogous to their translational counterparts—and measured in different units.
Brain Snack
A common machine that turns rotational kinetic energy into translational kinetic energy is the pitching machine—spinning wheels transfer energy to a baseball launched out of the front of the machine. Heat your heart out, Randy Johnson.
*Since torque is measured in N · m and angle in the dimensionless radian, the product of torque and angle also has units of N · m—where 1 N · m = 1 kg · m2/s2 = 1 J.
Like all forms of mechanical energy, rotational kinetic energy obeys the Law of Conservation of Energy. This means that, like the One Ring, it cannot be created or destroyed save for in the mighty fires of Mount Doom itself. We are, however, free to change rotational kinetic energy into other forms of mechanical energy as we so desire. (A catapult, for example, turns the rotational motion of the weapon's arm into translational motion of the projectile.)
Just like objects can have both kinetic and potential energy, nothing is preventing an object from having both translational kinetic energy and rotational kinetic energy. In fact, this is something pretty common—it's a form of motion called rolling.
What physicists call "rolling" happens when an object is rotating and moving translationally: think car tires, bicycles, bowling balls. You hit the gas pedal, push on the bike pedals, or hurl the bowling ball down the lane, and all three objects move translationally—but also spin around their central axis. You see them rollin', you best not be hatin'.
The total mechanical energy of a rolling object is equal to the sum of its translational kinetic energy (based on its translational speed v) and its rotational kinetic energy (based on its rotational speed ω), plus any potential energy it might have. This is different than objects that only spin—tops, hula hoops, gyroscopes—which will only have rotational kinetic energy, and objects that only slide, such as blocks on frictionless tables, which will only have translational kinetic energy. Rolling motion is the combination of the two.
Translational kinetic energy is given by
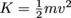 . Rotational kinetic energy, continuing our analogy quite nicely, is:
. Rotational kinetic energy, continuing our analogy quite nicely, is:
Energy is energy, though, and this is still measured in joules—check for yourself.
This means the total kinetic energy of any object is
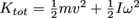 . For spinning objects, v = 0; for sliding objects, ω = 0. For rolling objects, neither v nor ω are zero.
. For spinning objects, v = 0; for sliding objects, ω = 0. For rolling objects, neither v nor ω are zero.Rotational Work
The concept of work in physics, recall, is blue collar in the extreme: forces show up, clock in, act continuously over a distance, then clock out and head home to their family. Work is a measure of an object's change in energy when a force acts on it—it is work that captures, for example, the change in kinetic energy of an accelerating car, based on the force exerted by the engine.
But what about the tires of the car? There is some work done speeding them from zero rpms to hundreds of rpms as the car accelerates, because the rotational kinetic energy of the tires changes. This change in rotational energy is called, appropriately enough, rotational work. Just as translational work is done by a force acting over a distance (W = Fd), rotational work is done by a torque acting over an angle:
Wrot = τθ
Since rotational work measures the change of rotational kinetic energy of an object as it is spun by some torque, there is also a work-energy theorem for rotational motion:
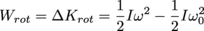
Here ω is an object's final angular velocity and ω0 is its starting angular velocity.
Rotational work and translational work are both measures of energy change, and so are both measured in joules.*
Rotational Power
If work can be extended to rotational motion as rotational work, then power—the rate at which an object can do work—must also have a rotational analog: rotational power.
While the basic definition is the same (power is power, and will always measure the rate at which an object can do work), we can calculate an object's power output by measuring its torque output. This is similar to translational motion, where an object's power is given by the force it can output multiplied by the speed it moves whatever that force acts on (P = Fv). Rotationally, the power of an object can be found by multiplying the torque it can output and the angular speed it moves whatever that torque acts on:
Prot = τω
But the two definitions of power measure the same thing. Imagine a winch, a device with ropes and pulleys used to hoist heavy objects.

Winch engines are often rated in horsepower, the same way car engines are. This is a measure of how fast the winch can do work—or, equivalently and more concretely, how fast the winch can lift things. A 2 hp (1492 W) engine can lift a 100 kg box at
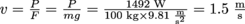 .
.If the pulley on the winch has a 10 cm radius, then to move that same 100 kg weight, it must turn a torque of
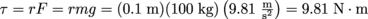 . It can turn this torque at a rate of
. It can turn this torque at a rate of 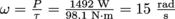 .
.15 rad/s on a pulley with a 0.1 m radius is equivalent to a tangential velocity of
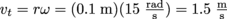 .
.Boom.
Common Mistakes
Rotational energy, work, and power are all convertible to their translational equivalents, and are measured in the same units. This is very different than angular velocity, acceleration, and momentum, which are all only analogous to their translational counterparts—and measured in different units.
Brain Snack
A common machine that turns rotational kinetic energy into translational kinetic energy is the pitching machine—spinning wheels transfer energy to a baseball launched out of the front of the machine. Heat your heart out, Randy Johnson.
*Since torque is measured in N · m and angle in the dimensionless radian, the product of torque and angle also has units of N · m—where 1 N · m = 1 kg · m2/s2 = 1 J.