Relativistic Mass, Energy, and Momentum
Since all of Newtonian physics relies on time and distance, we correctly anticipate that concepts dependent on time and distance change too. How do energy, work, force, and momentum change in special relativity? Buckle up: relativistic rides are out of this world. We mean that literally.
Does the law of inertia apply to energy too? In other words, does energy also have inertial mass?
Einstein's most famous equation E = mc2 describes just this. Energy is simply equal to mass times the speed of light squared. This is the relationship we use when we explained nuclear reactions8.
There's a thought experiment ("gedanken" to Einstein) that allows us to come to that conclusion ourselves.
Picture the following scenario. We have a box of mass M and length L that is at rest initially. The box emits a burst of photons from one end:

We learn from particle physics where relativistic speeds are the norm that the momentum of a photon is given by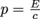 ,where E is the energy of that photon. Because of the law of conservation of momentum, the total momentum of the system consisting of a box plus photons must be zero. This means the box acquires a momentum equal and opposite to the photons',
,where E is the energy of that photon. Because of the law of conservation of momentum, the total momentum of the system consisting of a box plus photons must be zero. This means the box acquires a momentum equal and opposite to the photons', 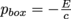 for each collision, and recoils a small distance Δx for each collision, just like the recoil of decaying particles.
for each collision, and recoils a small distance Δx for each collision, just like the recoil of decaying particles.
Since momentum is both p = Mv and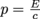 , we can write that
, we can write that 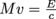 and solve for the recoil velocity v, such that
and solve for the recoil velocity v, such that 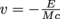 .
.
The photons reach the end of the box after traveling a distance equal to its length L. This occurs in a time interval Δt equal to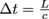 .
.
 >
>
When the photons reach the end of the box, the box recoils again by a distance Δx and returns to its original position. Since displacement is equal to velocity multiplied by time, or Δx = vΔt, we can write that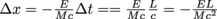 .
.
But did the center of mass of the box and its contents really move? Doesn't seem likely. What about the photons? What if there was some little mass m associated with light, such that the center of mass of the system didn't change? In this case, the center of mass C of the box would be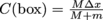 .The center of mass of the photons, C(photons), would be
.The center of mass of the photons, C(photons), would be 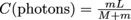 .Since the total center of mass doesn't change, we can add the two together and set it to zero, as it would be if the center of mass of the entire system stayed as it was.:
.Since the total center of mass doesn't change, we can add the two together and set it to zero, as it would be if the center of mass of the entire system stayed as it was.:
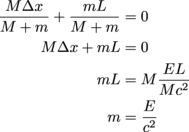
In other words, E = mc2.
This is known as the principle of mass-energy equivalence. Energy in any form has a mass equivalent. And if something has mass, then energy also has inertia.
If the energy of a relativistic particle increases, then mass has to go up too. As weird as this is, it's also a safeguard. It would take so much energy to get a massive object to a relativistic speed that it's unrealistic. Hence, today's space shuttles travel at a mere 0.00005c.
Anyways, since mass also increases at relativistic speeds with the total energy, we have a relativistic mass m and a rest mass, or proper mass, mo. As we might've guessed, they are related by our friend γ with the equation m = γmo, where γ is as usual equal to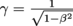 and
and 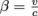 .
.
Since energy E is given by E = mc2, we'll also have to distinguish relativistic energy E and rest energy Eo. But what is relativistic energy, if not the energy associated with motion? Yes, we've seen this before. It's called kinetic energy, or K. In classical mechanics, kinetic energy is }. In special relativity, the total energy E is given by the rest energy plus the kinetic energy, such that K = E − Eo= mc2 − moc2 = (γ −1)moc2.
}. In special relativity, the total energy E is given by the rest energy plus the kinetic energy, such that K = E − Eo= mc2 − moc2 = (γ −1)moc2.
Lastly, in classical mechanics, we learned that the momentum of an object is equal to its velocity multiplied by its mass, or p = mv and that momentum is conserved. The conservation of momentum means it shouldn't change depending on a frame of reference. How can this hold true when we've just learned that velocities will transform from one frame to the other?
Since p = mv is only valid when v << c when the speed of the object is much, much less than the speed of light, just like the rest of Newtonian physics, we have to take into account the increased mass at relativistic speeds, or p = γmov.
Let's sum all this up in a list. Who doesn't love lists? Oh, put your hand down.
p = γmov
m = γmo
E = K + Eo = mc2Eo = moc2K = (γ – 1)moc2
The graph below shows the relationship between kinetic energy and velocity is different for Newtonian mechanics and special relativity, with the velocity expressed as a fraction of the speed of light, β. In special relativity, kinetic energy increases asymptotically to infinity as , because of Einstein's second postulate, the speed limit of the universe is c.
, because of Einstein's second postulate, the speed limit of the universe is c.
Any phenomenon that involves velocity in physics will be affected when speeds approach the speed of light. This means a quantity or vector will have two "sides": one measured at rest, such as rest mass and the other measured while moving, such as relativistic mass.
Particle physicists consider relativity all the time, as do astronomers, and as does every GPS device. Read all about relativity for a GPS system and more.
Einstein's Box
In Newtonian mechanics, we defined momentum as the product of mass and velocity, p = mu. We also associated mass with an amount of inertia, the tendency of an object to remain at rest or travel at constant velocity. The more mass, the more inertia.Does the law of inertia apply to energy too? In other words, does energy also have inertial mass?
Einstein's most famous equation E = mc2 describes just this. Energy is simply equal to mass times the speed of light squared. This is the relationship we use when we explained nuclear reactions8.
There's a thought experiment ("gedanken" to Einstein) that allows us to come to that conclusion ourselves.
Picture the following scenario. We have a box of mass M and length L that is at rest initially. The box emits a burst of photons from one end:

We learn from particle physics where relativistic speeds are the norm that the momentum of a photon is given by
 ,where E is the energy of that photon. Because of the law of conservation of momentum, the total momentum of the system consisting of a box plus photons must be zero. This means the box acquires a momentum equal and opposite to the photons',
,where E is the energy of that photon. Because of the law of conservation of momentum, the total momentum of the system consisting of a box plus photons must be zero. This means the box acquires a momentum equal and opposite to the photons',  for each collision, and recoils a small distance Δx for each collision, just like the recoil of decaying particles.
for each collision, and recoils a small distance Δx for each collision, just like the recoil of decaying particles. Since momentum is both p = Mv and
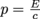 , we can write that
, we can write that 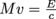 and solve for the recoil velocity v, such that
and solve for the recoil velocity v, such that 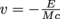 .
.The photons reach the end of the box after traveling a distance equal to its length L. This occurs in a time interval Δt equal to
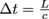 .
. >
>When the photons reach the end of the box, the box recoils again by a distance Δx and returns to its original position. Since displacement is equal to velocity multiplied by time, or Δx = vΔt, we can write that
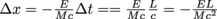 .
.But did the center of mass of the box and its contents really move? Doesn't seem likely. What about the photons? What if there was some little mass m associated with light, such that the center of mass of the system didn't change? In this case, the center of mass C of the box would be
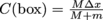 .The center of mass of the photons, C(photons), would be
.The center of mass of the photons, C(photons), would be 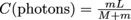 .Since the total center of mass doesn't change, we can add the two together and set it to zero, as it would be if the center of mass of the entire system stayed as it was.:
.Since the total center of mass doesn't change, we can add the two together and set it to zero, as it would be if the center of mass of the entire system stayed as it was.: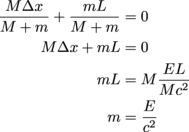
In other words, E = mc2.
This is known as the principle of mass-energy equivalence. Energy in any form has a mass equivalent. And if something has mass, then energy also has inertia.
Relativistic Mass, Kinetic Energy, and Momentum
The equation E = mc2 implies that mass has a connection to relativity, does it not? Let's talk more about that.If the energy of a relativistic particle increases, then mass has to go up too. As weird as this is, it's also a safeguard. It would take so much energy to get a massive object to a relativistic speed that it's unrealistic. Hence, today's space shuttles travel at a mere 0.00005c.
Anyways, since mass also increases at relativistic speeds with the total energy, we have a relativistic mass m and a rest mass, or proper mass, mo. As we might've guessed, they are related by our friend γ with the equation m = γmo, where γ is as usual equal to
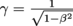 and
and 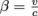 .
.Since energy E is given by E = mc2, we'll also have to distinguish relativistic energy E and rest energy Eo. But what is relativistic energy, if not the energy associated with motion? Yes, we've seen this before. It's called kinetic energy, or K. In classical mechanics, kinetic energy is
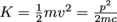 }. In special relativity, the total energy E is given by the rest energy plus the kinetic energy, such that K = E − Eo= mc2 − moc2 = (γ −1)moc2.
}. In special relativity, the total energy E is given by the rest energy plus the kinetic energy, such that K = E − Eo= mc2 − moc2 = (γ −1)moc2.Lastly, in classical mechanics, we learned that the momentum of an object is equal to its velocity multiplied by its mass, or p = mv and that momentum is conserved. The conservation of momentum means it shouldn't change depending on a frame of reference. How can this hold true when we've just learned that velocities will transform from one frame to the other?
Since p = mv is only valid when v << c when the speed of the object is much, much less than the speed of light, just like the rest of Newtonian physics, we have to take into account the increased mass at relativistic speeds, or p = γmov.
Let's sum all this up in a list. Who doesn't love lists? Oh, put your hand down.
p = γmov
m = γmo
E = K + Eo = mc2Eo = moc2K = (γ – 1)moc2
The graph below shows the relationship between kinetic energy and velocity is different for Newtonian mechanics and special relativity, with the velocity expressed as a fraction of the speed of light, β. In special relativity, kinetic energy increases asymptotically to infinity as
 , because of Einstein's second postulate, the speed limit of the universe is c.
, because of Einstein's second postulate, the speed limit of the universe is c.
Any phenomenon that involves velocity in physics will be affected when speeds approach the speed of light. This means a quantity or vector will have two "sides": one measured at rest, such as rest mass and the other measured while moving, such as relativistic mass.
Particle physicists consider relativity all the time, as do astronomers, and as does every GPS device. Read all about relativity for a GPS system and more.