Test Your Knowledge
Newtonian Physics
1. Carbon-14 decays to nitrogen-14 with a half-life of τ= 5730 years9. If we used a carbon atom to measure our 1-mile run, how long would our 10-minute run last?2. How long does our run in #1 last in units of carbon half-lives?
3. Light travels at a speed of
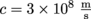 .What is our velocity from #1 as a fraction of c?
.What is our velocity from #1 as a fraction of c?4. Mr. Gaspard, the mean neighbor, comes out of his house before we reach the trashcan. Appalled, he begins to run towards us muttering something about " devilish rascals going through his trash and making messes". Mr. Gaspard is clumsy, but as a Navy veteran he's still fast.. His velocity is ux(G) = 0.2 miles per minute. As he runs towards us, what is hisvelocity from ourframe of reference as we continue to run at half that speed but in the opposite direction?
5. Let S and S' now be frames of references for Igor and us, respectively. We both start off at position (x, y, z) = (x', y', z') = (0, 0, 0). What is our position in Igor's frame of reference S exactly one hour later?We're running at a velocity of ux = 6 mph while Igor moves with velocity ux(IGOR) = 4 mph.
1. Answer: The answer is still Δt = 10 minutes. It doesn't matter what kind of clock we use: 10 minutes is 10 minutes is 10 minutes.
2. Answer: A carbon half-life is τ = 5730 years. We measured the run in minutes, so we convert these years to minutes.
Converting the half life from years to minutes, we take
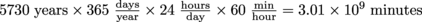 . The run lasted 10 minutes. In terms of the half life, our run lasts
. The run lasted 10 minutes. In terms of the half life, our run lasts 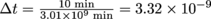 carbon half-lives.
carbon half-lives. 3. Answer: Your velocity is 1 mile in 10 minutes, 0.1. The speed of light in miles per minute is
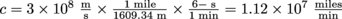 .Therefore the ratio is
.Therefore the ratio is 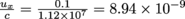 }, such that our velocity ux is equal to ux = 8.94 × 10-9c.
}, such that our velocity ux is equal to ux = 8.94 × 10-9c. Hey, that's the definition of β, so β = 8.94 × 10-9.
4. Answer:We're also running and we're moving towards each other, so the distance between us is shortened at a faster rate than if one of the two parties stood still. In this case, we need to add both our velocity and his together, which gives you a relativevelocity of v = -0.2 − 0.1 = =0.3 miles per minute. Since we haven't defined which direction is the positive one, either sign will do. Velocities relative to whom? Well, to each other.
5. Answer: Remember that what matters is the velocity v of two frames relative to each other. We defined this earlier on as the difference between your two velocities, v = 6 − 4 = 2 mph. That's the velocity we need to find the coordinates.
Next, we consider that only the x-direction changes, and that y and z will remain 0. We find the change in x by x = x' + vt = 0 + (2 mph)(1 hr) = 2 miles. Our entire spatial coordinates are (x, y, z) = (2, 0, 0). If we add t = 1 hourto these three physical dimensions, we have space-time coordinates of (x, y, z, t) = (2, 0, 0, 1). Space-time coordinates are what gave rise to the saying "Time is the fourth dimension."
Alternatively we could find the positions of both Igor and ourselves at 1 hour and take the difference between them, but since we used relative velocity we achieved the same result.
Special Relativity
1. You decide to take revenge and kick Gaspard's trashcan over in the dark of night. As we approach his house, he springs out of the bushes with a flashlight. He begins to run towards us at a velocity of ux(G) = 10 mph. The man never tires. We bolt the other way at a velocity of ux = 6 mph. What is the speed of light in each frame of reference?2. The Albertian is moving at a velocity of half the speed of light c. Calculate the relativistic factor associated with our brand new spaceship.
3. If Gaspard measures a relativistic time of Δt = 10 seconds for an event aboard The Albertian still moving at 0.5c, what is the proper time Δto that we measure for the same event aboard The Albertian?
4. We arrive at another train station in the luxurious one-bulb merchandise wagon aboard Train Shmoop. We gasp to see that Gaspard has thrown himself onto a cart in the back and has arrived here with us. However, the merchandise train is exporting a brand new line of relativistic cars. We jump into a car that travels at a speed of 0.98c. Gaspard follows you in another car that travels at a speed of 0.95c. What are ours and Gaspard's relative velocities with respect to the train station?
5. The merchandise train on which we escaped earlier was built by super engineers. The train itself can go up to half the speed of light. How long does the cart measure a) according to us and b) according to Gaspard, left behind at the station? A beam of light spends 20 ns traveling half the length of the cart, 0.5Lo.
1. Answer: We saw in our description of the Michelson-Morley experiment that the speed of light c is constant, or universal. And it's Einstein's second postulate: It doesn't matter whose frame of reference c is in, it's always going to stay the same
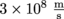 .
.2. Answer: There's no need to divide
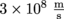 by 2 because all we care about is the fraction
by 2 because all we care about is the fraction 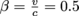 .Actually, we care about β to get to γ, which in turn is
.Actually, we care about β to get to γ, which in turn is 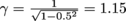 .
.3. Answer: We already calculated our relativistic factor as γ = 1.15 in #2. Knowing that Δt = γΔto,we solve for Δto = 8.70 seconds .
The event, whatever it is, lasts 8.7 s according to us, and 10 seconds according to Gaspard.
4. Answer: Your speeds are measured with respect to the train station. This means that according to us, the train station takes off with a velocity of u' = -0.98c, and according to Gaspard, the train station takes off with a velocity of u = -0.95c. The relative velocity between us and Gaspard is given by v in
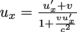 and
and 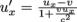 .Great, v is inaccessible in each. Oh, that means we need
.Great, v is inaccessible in each. Oh, that means we need 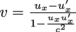 .
.Plugging in our numbers, which may all be left in terms of c, we get
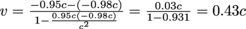 .
.For a seemingly small difference in velocities 0.98c and 0.95c, Gaspard and ourselves move at the surprisingly large v = 0.43c relative to one another.
5. Answer: a) Since the speed of light is always
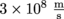 and length is given by speed multiplied by time, Lo is equal to L_{o} = 2 \times
and length is given by speed multiplied by time, Lo is equal to L_{o} = 2 \times 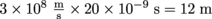 That's the proper length according to us, in the same frame of reference as the light.
That's the proper length according to us, in the same frame of reference as the light.b) We calculated earlier, but could calculate again, that a speed of 0.5c results in a gamma factor of γ = 1.15. We use
h3>Relativistic Mass, Energy, and Momentum
1. An electron's mass is 9.11 × 10-31 kg. What is its associated energy E in keV (kilo electron-volts)? One Joule is 1.6 × 1019 eV.
2. What is the mass of an electron traveling at 0.75c in
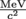 if the proper mass of the electron is
if the proper mass of the electron is 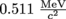 ?
?3. Check to seethat p = γmu becomes p = mu when u << c.
4. How much energy is needed to accelerate an object to the speed of light, if the object is traveling at a velocity of u = 0.99c?
5. Use the momentum and energy equations to find a relation between total energy E and momentum p.
1. Answer: Using E = mc2, we can write E = (9.11 × 10-31 kg)(
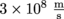 )2 = 8.20 × 10-14 Joules. Since 1 J = 1.6 × 1019 eV, after multiplying the two to convert the energy into eV we get the electron's energy as E = 5.11 × 105 eV, or E = 511 keV.
)2 = 8.20 × 10-14 Joules. Since 1 J = 1.6 × 1019 eV, after multiplying the two to convert the energy into eV we get the electron's energy as E = 5.11 × 105 eV, or E = 511 keV.2. Answer: Since E = mc2, we see how using units of
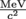 }for mass would simplify the math. For β = 0.75, γ = 1.51. Relativistic mass is
}for mass would simplify the math. For β = 0.75, γ = 1.51. Relativistic mass is 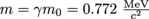 .
.3. Answer: If u << c, then β is incredibly small, near 0.Gamma is then near 1, so p = mu.
4. Answer: We are basically asking what change of energy is needed to go from u = 0.99c to u = c. If we stick u = c into our gamma equation, we get 1 over 0, which is undefined. It's impossible to lend enough energy for an object with mass to reach the speed of light.
5. Answer: Knowing that E = mc2where m is the relativistic mass, we write
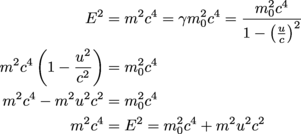
Then, since p = γmou = mu where m is the relativistic mass, we end up with a final equation for E2:
E2 = p2c2 + (moc2)2.