The First Law of Thermodynamics
Conservation of Energy
The First Law of Thermodynamics is "Do not talk about thermodynamics." Whelp. Lesson over, we guess.Just kidding. The first law actually says that energy can't just disappear (or appear out of nowhere). It is conserved.
It also says that any "system" we observe, like, say, that Helium balloon we've been carrying along, contains three different types of energy.
- Internal energy, U: This is the energy of all of the molecules zipping around in a system. Let's take the example of a pot of hot water. As we heat up the water, the energy of the water molecules increases and they start moving faster. We just learned how pressure, volume, and temperature relate to the speed of these atoms. The kinetic energy of the molecules in the pot is called the internal energy, U, of the system.
- Heat, Q: Next we have the thermal energy transfer. This is just a fancy way of saying that if our water molecules move really, really fast, the temperature of the water will rise. When we put the pot on the stove, we can touch the pot. As the water molecules start moving faster and the temperature of the water rises, we can still touch the pot, but it's not recommened. Wicked burns much? Energy is transferred from the water molecules in the pot to our hands in the form of heat, Q.
- Work, W: Let's remove our hands from that boiling pot of water and instead place a lid on it. As the water boils more vigorously, and more water experiences a phase change and vaporizes, the lid on the pot starts rattling. The steam is doing work, W: it's lifting the lid of the pot.
There are too many things that the water can do in our boiling pot of water system to consider the system "closed." Energy is still conserved, but you would need a very fancy equation to account for that big puddle on the windowsill.
Get To Work
Instead we'll consider a simpler system, like a confined ideal gas. A great example is our trusty old Helium balloon. For a confined ideal gas the first law of thermodynamics says that ΔU = Q + W. Can we get that again, in English?The change in the internal energy of the system, ΔU, or the change in how fast the molecules in our helium balloon are moving, depends on how much energy is transferred as mechanical work, W, and as heat, Q. Well there we go.
Watch out—this first law of thermodynamics equation is sometimes written with different signs. It all depends on the sign convention (positive or negative) for work, W. The equation above labels the heat, Q, and work, W, as positive when energy is put into the system. When we compress our Helium balloon and heat it, then both Q and W are positive. Switch the convention around, and we need to switch the signs, too.
So how do we calculate how much work is done on our system, the helium balloon? It sure doesn't fill out a time card after each shift, that's for sure. Instead, the amount of work is related to how much we compress the balloon (which raises the pressure, P) and on how much we change the volume of the balloon, ΔV. Here's the equation.
W = -P ΔV
The work we do on the balloon, or how much energy we have to exert to compress it, depends on how much we want to compress it and on how much the volume changes. Let's say we want to compress the balloon until it is half the volume it was before. (What can we say, we're in a Hulk smash kind of mood.)
This would take a lot of pressure, P, if the balloon we'd just blown that balloon up. It would take a lot less pressure if the balloon was on day 7 of its post-birthday party decline. So the total amount of work we do is different in the two scenarios, even though we're cutting the volume in half each time. We have to take the difference in volume, not the ratio of volumes, for the work equation.
When we go to compress the balloon, it's pretty easy at first. The smaller the balloon gets, though, the harder it is to compress it even further. It doesn't get to be actually hard, but still. The amount of work we have to do changes as we compress it further. It's kind of like school—the further into the year we get, the more the pressure builds, until we're trying to cram for five final exams at the last second.
Draw A Picture; It'll Work Longer
To account for all these changes in pressure and volume, we draw PV diagrams, like this one.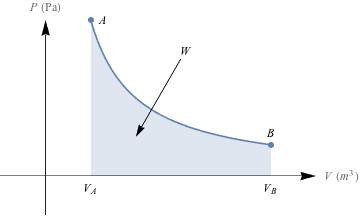
As we compress the balloon from volume VA, to VB, the pressure changes. The amount of work, W, done is equal to the area under the PV curve. Unless you've already got some calculus under your belt, it's a pain and a half to find this kind of area, so we'll just sidestep the issue for now.
So how much work is done when we change the pressure of a gas without affecting its volume? It's Picasso time—let's draw a PV graph for this scenario.
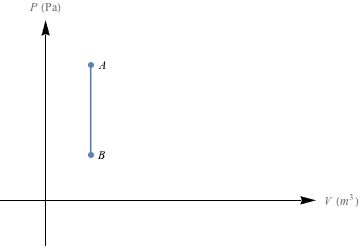
The area under this PV curve is zero – no work is done here. It's useless. Well, for work.
One final example: In which case do you think we're doing more work?
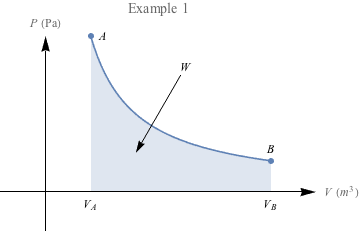
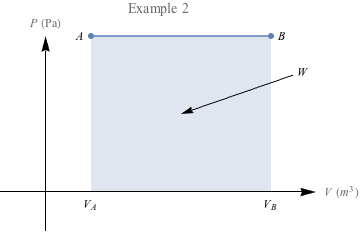
The area under the second PV diagram is much larger, suggesting that a lot more work is required to reach the larger volume under constant pressure. There's a special name for work under constant pressure like this: isobaric.
When pressure remains constant, we have an isobaric process. This makes our calculations easy-peasy, because we can apply the first law of thermodynamics without having to do any calculus, just W = -PΔV and ΔU = W + Q.
The process in the first example we discussed, with constant volume while the pressure changes in the gas, is called an isovolumetric or isochoric process. Now give us a second to untie our tongue.
Okay. We already determined that W = 0 in such a volume-saving process, so ΔU = W + Q simplifies to ΔU = Q.
We could also change the volume of a gas while keeping the temperature constant. This is an isothermal process (not to be confused with thermal underwear). Since the temperature reflects the internal energy of the gas, or how fast the molecules of the gas are moving, ΔU = 0. In this case, ΔU = W + Q simplifies to W = -Q.
All of the work done on this type of system is transferred into heat, Q. Calculating the amount of work for this case requires a fancier equation than the others. It is
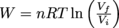 , where n is the number of moles of gas, R is the gas constant, T is temperature, and V is volume. It left the top hot and monocle at home, though.
, where n is the number of moles of gas, R is the gas constant, T is temperature, and V is volume. It left the top hot and monocle at home, though.Lastly, a process can also be adiabatic. In this case, there is no exchange of heat between the gas and the environment (which means there's some kicking insulation installed),, so Q = 0 and ΔU = W + Q, which simplifies to ΔU = W. Nice, nice. We can then determine the work itself by
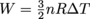 . Again, this is for adiabatic processes only. Try to use this equation on a diabatic process, and it'll go into diabatic shock.
. Again, this is for adiabatic processes only. Try to use this equation on a diabatic process, and it'll go into diabatic shock.Common Mistakes
There are two ways to write the first law of thermodynamics. The way we wrote it, ΔU = W + Q, follows a sign convention where work done by the system is negative. Some textbooks will write the first law as ΔU = Q – W. In this case, work done by the system is positive.In both cases, heat, Q, is positive when it is put into the system and negative when it leaves the system. Be sure to put in the work to know what kind of work you're doing, or you'll be working overtime to fix your mistakes.
