Simple Harmonic Motion
We know, this learning guide focuses on waves. But think of simple harmonic motion like the gentle training swells before tackling big wave surfing. Beach Boys’ music is still allowed.
"Simple harmonic motion" is the term we use to describe the motion of an object where the net force is proportional to the object's displacement from equilibrium. Imagine a block sitting on a (frictionless) table, tethered to a wall by a spring.

The block is perfectly happy to sit still in the middle of the table, until you pull it an inch or two away from the wall. Then, the spring tries to pull the block back—but without friction, it pulls too far and the block ends up compressing the spring.
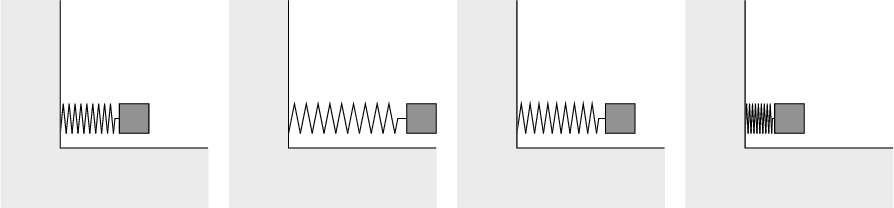
The compressed spring pushes the block out again, past equilibrium, until it reaches a point where the now-stretched spring pulls the block back and starts the cycle over again. The block will keep oscillating like this back and forth forever—until it's stopped by an outside force.

Simple harmonic motion arises in a lot of different situations, but the basics always follow this pattern: an object is disturbed from equilibrium, a force pulls it back too far, and it repeats. Again and again and again. Think of blocks on springs, pendulums, even charged particles in electric or magnetic fields.

Hooke's Law gives us F = -kx. The force on the block is inversely proportional to where the block is. As it moves right, the force pulls it left; but as it moves too far left, the force pushes it back to the right.
After it starts to oscillate at time t = 0, the position x of the block at any time t can be given by a simple equation:
x(t) = Acos(ω t + φ)
Okay, maybe simple is an understatement. Let's unpack this a little. This equation means that our back-and-forth motion of the block can be described exactly by a cosine wave—the same kind you've talked about in your trigonometry class.*
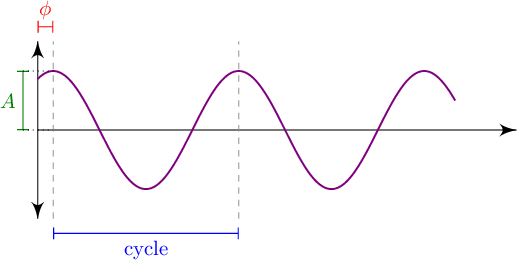
A is the amplitude, the max distance the block ever travels away from equilibrium (how far you stretch the spring, measured in meters). Inside the cosine, ω is the motion's angular frequency (how fast the block moves back and forth, measured in rad/s). Finally, φ is the wave's phase (where on the wave the block starts, measured in radians).
These three variables represent some of the most important descriptions of a wave, and we'll be spending a lot more time on them throughout the chapter.
The final thing to note is a wave's cycle. This is the part of the motion that repeats—for a cosine wave, it's the "V" shaped dip that shows up over and over and over.
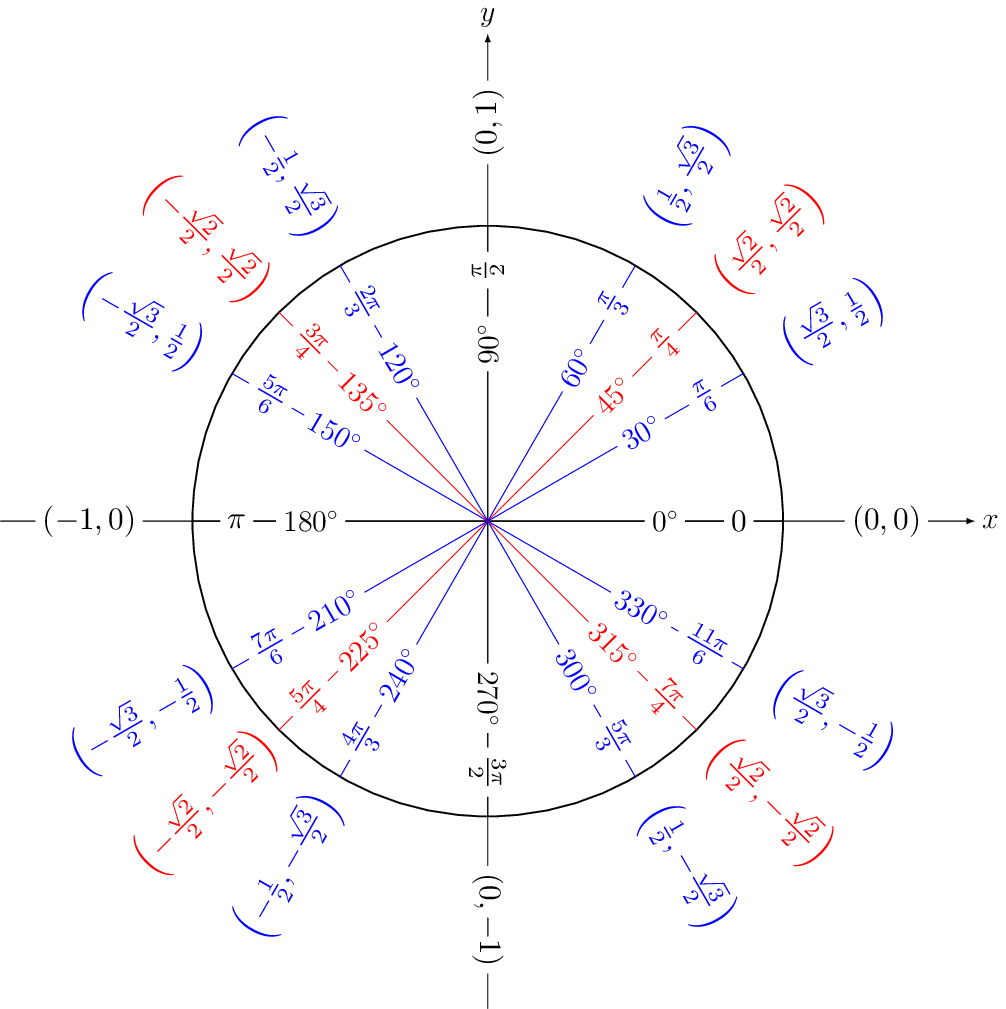
In this drawing, the x number gives the value of a cosine wave (of amplitude 1) for a given angle between 0 and 2π rad. So if you imagine a ball rolling around this circle, it passes through all the values cosine reaches: if it's rolling at 1 rad/s, starting at t = 0 it would be at (1,0); at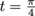 it would be at
it would be at 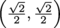 at t = π it would be at (0,1). Mathematically, there's no difference between the wave and the circle. Cool, right? Kinda? Anyone?
at t = π it would be at (0,1). Mathematically, there's no difference between the wave and the circle. Cool, right? Kinda? Anyone?
Rotation—where an object goes around and around and around on the same path—is repetitive motion. And repetitive motion is wave motion. Up and down, left and right, round and round... it's all just sine and cosine waves. This is why wave motion (any wave motion) can be measured in radians and rad/s, even if there's no rotational motion at all.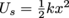 and all that), so the spring can never have more potential energy than right now, as it's stretched to 5 cm. That means when you let go, the spring will never be able to extend (or compress) more than 5 cm—this is our motion's amplitude.
and all that), so the spring can never have more potential energy than right now, as it's stretched to 5 cm. That means when you let go, the spring will never be able to extend (or compress) more than 5 cm—this is our motion's amplitude.
We know at t = 0 that x(0) = 5 cm, so we can figure out φ: x(t) = Acos(ωt + φ) → x(0) = (5 cm)cos(ω × (0 s) + φ) → 5 cm = (5 cm)cos(φ) → 1 = cos(φ). This is only true when φ = 0 rad,** so we know that the motion of our block is given by x(t) = 5cos(ω t).
Figuring out the frequency of the wave is trickier—it's very dependent on what's causing the motion. For a spring-block system like ours (and only for a spring-block system!) the frequency is dependent on the mass of the block (m) and the stiffness of the spring (k): . For a 1 kg block and a 100 N/m spring, the frequency of oscillation will be
. For a 1 kg block and a 100 N/m spring, the frequency of oscillation will be 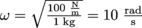 .
.
Putting it all together, the whole motion of our block is described by one equation: x(t) = 5cos(10t).
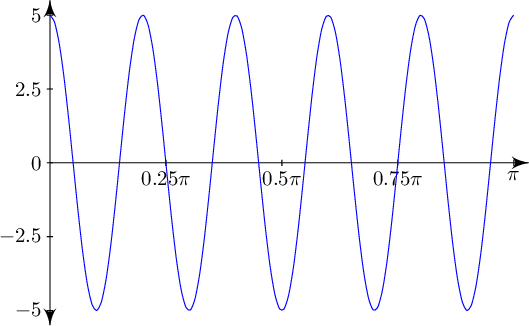
Simple-ish, right?
The kid's angular frequency is trickier—how many radians does she swing through per second? Well, if she's swinging at 1 Hz, she's completing one cycle per second. There are 2π rad in each cycle, so her angular frequency must be 2π rad/s. In other words, we can convert between frequency and angular frequency by multiplying by 2π, the number of radians in a cycle:
ω = 2πf
...which should hertz your head less to look at. (Don't worry, we'll show ourselves out.)
Brain Snack
For a pendulum, the frequency of the swing is dependent on the length of the string (not m or k like the block on a spring). But don't worry, it can still get really trippy.
*WARNING: calculus aside. If you're wondering why this happens to be true, look at Hooke's Law. Another way to write F = -kx is to replace F with ma, so that we have ma = -kx or . We know that acceleration is really the second derivative of position, so this can be written as
. We know that acceleration is really the second derivative of position, so this can be written as 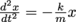 . What are the only functions x(t) that fit this pattern—functions whose second derivative is the same as the original function multiplied by a negative constant? The answer: trig functions sine and cosine.
. What are the only functions x(t) that fit this pattern—functions whose second derivative is the same as the original function multiplied by a negative constant? The answer: trig functions sine and cosine. 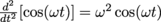 .
.
**Or φ = 2π, but keep it as simple as possible.
"Simple harmonic motion" is the term we use to describe the motion of an object where the net force is proportional to the object's displacement from equilibrium. Imagine a block sitting on a (frictionless) table, tethered to a wall by a spring.

The block is perfectly happy to sit still in the middle of the table, until you pull it an inch or two away from the wall. Then, the spring tries to pull the block back—but without friction, it pulls too far and the block ends up compressing the spring.
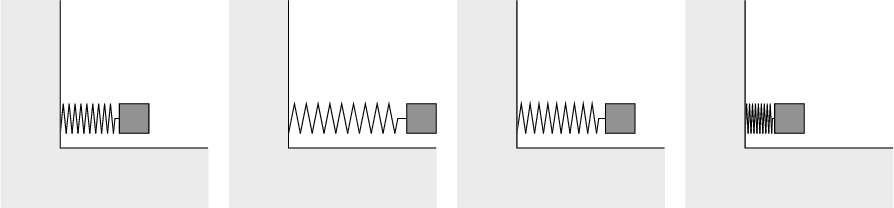
The compressed spring pushes the block out again, past equilibrium, until it reaches a point where the now-stretched spring pulls the block back and starts the cycle over again. The block will keep oscillating like this back and forth forever—until it's stopped by an outside force.

Simple harmonic motion arises in a lot of different situations, but the basics always follow this pattern: an object is disturbed from equilibrium, a force pulls it back too far, and it repeats. Again and again and again. Think of blocks on springs, pendulums, even charged particles in electric or magnetic fields.
Describing SHM with Trig Functions
In our block-and-spring example, the forces look like this:
Hooke's Law gives us F = -kx. The force on the block is inversely proportional to where the block is. As it moves right, the force pulls it left; but as it moves too far left, the force pushes it back to the right.
After it starts to oscillate at time t = 0, the position x of the block at any time t can be given by a simple equation:
x(t) = Acos(ω t + φ)
Okay, maybe simple is an understatement. Let's unpack this a little. This equation means that our back-and-forth motion of the block can be described exactly by a cosine wave—the same kind you've talked about in your trigonometry class.*
A is the amplitude, the max distance the block ever travels away from equilibrium (how far you stretch the spring, measured in meters). Inside the cosine, ω is the motion's angular frequency (how fast the block moves back and forth, measured in rad/s). Finally, φ is the wave's phase (where on the wave the block starts, measured in radians).
These three variables represent some of the most important descriptions of a wave, and we'll be spending a lot more time on them throughout the chapter.
The final thing to note is a wave's cycle. This is the part of the motion that repeats—for a cosine wave, it's the "V" shaped dip that shows up over and over and over.

Trig Functions and Rotation
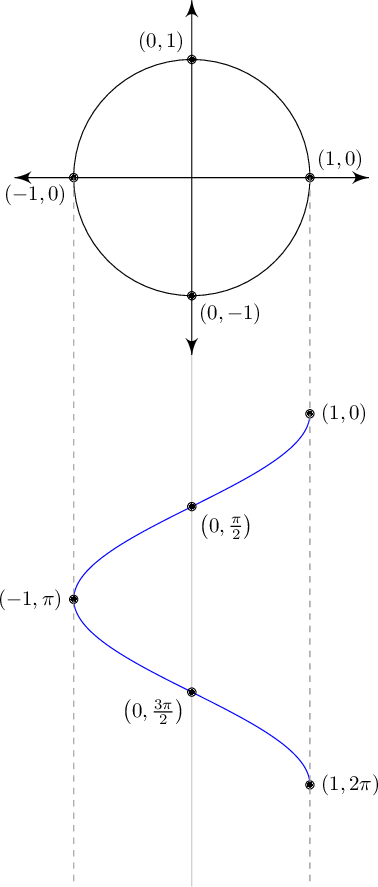
Now we're talking about a spring and a block and a very linear motion on a table. You might be wondering where all the radians, something we've only seen in rotational motion, are coming from. The truth is there are a lot of similarities between cosine waves and rotation. Remember the unit circle from math class?
In this drawing, the x number gives the value of a cosine wave (of amplitude 1) for a given angle between 0 and 2π rad. So if you imagine a ball rolling around this circle, it passes through all the values cosine reaches: if it's rolling at 1 rad/s, starting at t = 0 it would be at (1,0); at
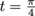 it would be at
it would be at 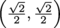 at t = π it would be at (0,1). Mathematically, there's no difference between the wave and the circle. Cool, right? Kinda? Anyone?
at t = π it would be at (0,1). Mathematically, there's no difference between the wave and the circle. Cool, right? Kinda? Anyone?
Rotation—where an object goes around and around and around on the same path—is repetitive motion. And repetitive motion is wave motion. Up and down, left and right, round and round... it's all just sine and cosine waves. This is why wave motion (any wave motion) can be measured in radians and rad/s, even if there's no rotational motion at all.
The Spring Revisited
For now, let's focus on the fancy shmancy block on a spring. At time t = 0, you pull the block 5 cm away from equilibrium, stretching the spring. Energy stored in a spring is all based on the length the spring has been stretched (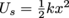 and all that), so the spring can never have more potential energy than right now, as it's stretched to 5 cm. That means when you let go, the spring will never be able to extend (or compress) more than 5 cm—this is our motion's amplitude.
and all that), so the spring can never have more potential energy than right now, as it's stretched to 5 cm. That means when you let go, the spring will never be able to extend (or compress) more than 5 cm—this is our motion's amplitude.We know at t = 0 that x(0) = 5 cm, so we can figure out φ: x(t) = Acos(ωt + φ) → x(0) = (5 cm)cos(ω × (0 s) + φ) → 5 cm = (5 cm)cos(φ) → 1 = cos(φ). This is only true when φ = 0 rad,** so we know that the motion of our block is given by x(t) = 5cos(ω t).
Figuring out the frequency of the wave is trickier—it's very dependent on what's causing the motion. For a spring-block system like ours (and only for a spring-block system!) the frequency is dependent on the mass of the block (m) and the stiffness of the spring (k):
 . For a 1 kg block and a 100 N/m spring, the frequency of oscillation will be
. For a 1 kg block and a 100 N/m spring, the frequency of oscillation will be 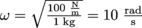 .
.Putting it all together, the whole motion of our block is described by one equation: x(t) = 5cos(10t).

Simple-ish, right?
Angular Frequency and Frequency
10 rad/s is, admittedly, a pretty obscure number of rotations. To get a more intuitive sense of what this means, we can convert angular frequency to good old ordinary frequency. Frequency is measured in hertz, where 1 Hz = 1 s-1. Whereas angular frequency measures the number of radians the wave motion describes, frequency measures the number of cycles—how many times our wave does its dance. For example, a kid in a swing set may swing back and forth once per second. That's a frequency of 1 Hz. Done.The kid's angular frequency is trickier—how many radians does she swing through per second? Well, if she's swinging at 1 Hz, she's completing one cycle per second. There are 2π rad in each cycle, so her angular frequency must be 2π rad/s. In other words, we can convert between frequency and angular frequency by multiplying by 2π, the number of radians in a cycle:
ω = 2πf
...which should hertz your head less to look at. (Don't worry, we'll show ourselves out.)
Brain Snack
For a pendulum, the frequency of the swing is dependent on the length of the string (not m or k like the block on a spring). But don't worry, it can still get really trippy.
*WARNING: calculus aside. If you're wondering why this happens to be true, look at Hooke's Law. Another way to write F = -kx is to replace F with ma, so that we have ma = -kx or
 . We know that acceleration is really the second derivative of position, so this can be written as
. We know that acceleration is really the second derivative of position, so this can be written as 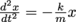 . What are the only functions x(t) that fit this pattern—functions whose second derivative is the same as the original function multiplied by a negative constant? The answer: trig functions sine and cosine.
. What are the only functions x(t) that fit this pattern—functions whose second derivative is the same as the original function multiplied by a negative constant? The answer: trig functions sine and cosine. 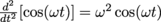 .
.**Or φ = 2π, but keep it as simple as possible.