Test Your Knowledge
Simple Harmonic Motion
1. What is the amplitude of the oscillation of a block-spring system that's initially compressed 1 cm?2. What is the phase of an oscillating block-spring system that passes through its furthest compressed point at time t = 0 s?
3. A 4 kg block is attached to a spring with a stiffness of 10 N/m. If the block is pulled out 3 cm and released on a frictionless table, at what point relative to its equilibrium position will the block be at after 5 seconds?
4. A pendulum, like the swinging weight under a grandfather clock, can also be an example of simple harmonic motion, but since there's no spring and no spring stiffness the angular frequency is given by a different formula:
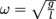 , where l is the length of the pendulum (the mass of the pendulum doesn't matter). How long does a clock pendulum need to be in order to swing once per second?
, where l is the length of the pendulum (the mass of the pendulum doesn't matter). How long does a clock pendulum need to be in order to swing once per second?5. A musical note used frequently for tuning instruments is an A, which clocks in at 440 Hz. What is this note's equivalent angular frequency?
Waves
1. When you throw a rock into a pond (or a child into a swimming pool, for our more suburban readers), the impact creates ripples that spread outward in a circle. Are these ripples transverse waves or longitudinal?2. What is the period of the motion of an LP record that spins at 33.3 rpm?
3. What is the period of a point right next to the center of the record? What about a point on the outside edge of the record? Which point moves faster?
4. All visible light waves move at the same speed (conveniently referred to as the speed of light, or c), where c = 3×108 m/s. How many times faster than red light (650 nm wavelength) does blue light (450 nm wavelength) oscillate?
5. What is the period of a pendulum 1 m in length? (Remember that for a pendulum
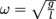 .)
.)Standing Waves and Interference
1. A standing wave in a 2 m long string has a wavelength of 1 m. How many antinodes does it have, and where are they located?2. At what time after t = 0 will a standing wave with frequency 60 Hz return to its original shape?
3. What is the resulting wave when these two waves interfere with one another?
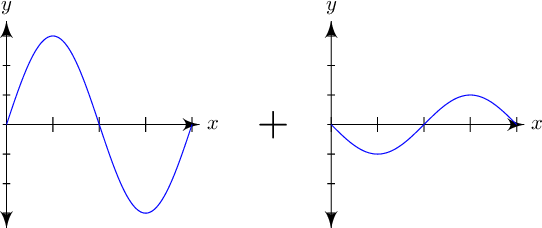
4. A string is shaken such that two traveling waves appear on opposite ends: one,
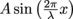 , starts on the left and travels to the right, and another,
, starts on the left and travels to the right, and another, 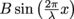 , starts on the right and travels left. What is the wave that results from the two traveling waves interfering with each other? Is it a standing wave?
, starts on the right and travels left. What is the wave that results from the two traveling waves interfering with each other? Is it a standing wave?5. The standing waves that arise in pipe organs are a different shape than guitar strings—while a guitar string is pinned on each end so that the endpoints become nodes, making the standing wave look like a sine, the air inside an organ pipe is constrained so that the antinodes are at the endpoints. This makes pipe organ standing waves look like cosines instead of sines, and the formula describing the wave then becomes:
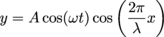
Sketch the wave created in a 1.54 m pipe at time t = 0 when the sound waves resonate with a frequency of 440 Hz. The speed of sound in air is about 340 m/s.
The Doppler Effect
1. If an ambulance siren has a nominal frequency of 500 Hz, what frequency will it appear to be as the ambulance drives up behind you at 40 miles per hour (about 17.88 m/s)?2. What is the wavelength of the observed sound as the ambulance in the previous question drives away from you at the same speed?
3. Once the ambulance gets to the hospital, it parks—but the siren keeps ringing for a few seconds. If you drive past the hospital, does the siren sound the same to you as to the ambulance driver? If not, as you approach the hospital, how is the siren's frequency shifted?
4. The radar guns wielded by highway patrol officers, that are the bane of any race car driver or Fast and Furious enthusiast, use a technology called Doppler radar. They make use of the Doppler Effect and radio waves (a form of electromagnetic radiation, just like visible light or microwaves) to measure the speed of a moving object.
The radio waves travel at the speed of light (called c, around 3×108 m/s) out of the gun and towards an object moving at speed v, then bounce off and are reflected back towards the gun with a different frequency than when they left. This difference in frequency is proportional to the speed of the moving object, given by
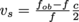 .
.What is the observed frequency when a 30 GHz radar beam is sent at a car traveling towards the police at 40 m/s?
5. If both the source of a wave and the observer of the wave are moving, the Doppler Effect still holds, but with one extra term. As an ambulance passes you at speed vs while you're on the road driving at speed vob, the frequency you hear will be
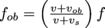 . For our 500 Hz ambulance siren passing you while moving at 17.88 m/s, what will the frequency you hear be if you're driving at 12 m/s?
. For our 500 Hz ambulance siren passing you while moving at 17.88 m/s, what will the frequency you hear be if you're driving at 12 m/s?Answers
Simple Harmonic Motion
1. What is the amplitude of the oscillation of a block-spring system that's initially compressed 1 cm?Without frictional losses, the amplitude of oscillation will be equal to the initial displacement—in this case, 1 cm.
2. What is the phase of an oscillating block-spring system that passes through its furthest compressed point at time t = 0 s?
Our equation for the block's motion is x(t) = Acos(ω t + φ). At t = 0, we know the position of the block is its most compressed state—in other words, x(0) = -A. Our equation for x gives us x(0) = Acos(ω × 0 + φ) = Acos(φ). Putting these together, we get -A = Acos(φ), or cos(φ) = -1. This is only true when φ = π rad.
3. A 4 kg block is attached to a spring with a stiffness of 10 N/m. If the block is pulled out 3 cm and released on a frictionless table, at what point relative to its equilibrium position will the block be at after 5 seconds?
The system's frequency is
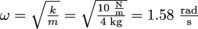 . With an initial displacement of 3 cm, the block's motion is described by the equation x(t) = (3 cm)cos((1.58 rad/s)t + φ). Since x(0) = 3 and we know x(0) = 3cos(1.58 × 0 + φ) = 3cos(φ), φ must equal 0 rad, giving us a final equation for the block's motion: x(t) = 3cos(1.58t). At t = 5 s, the block's position relative to equilibrium is x(5) = (3 cm)cos((1.58 rad/s) × (5 s)) = -0.14 cm.
. With an initial displacement of 3 cm, the block's motion is described by the equation x(t) = (3 cm)cos((1.58 rad/s)t + φ). Since x(0) = 3 and we know x(0) = 3cos(1.58 × 0 + φ) = 3cos(φ), φ must equal 0 rad, giving us a final equation for the block's motion: x(t) = 3cos(1.58t). At t = 5 s, the block's position relative to equilibrium is x(5) = (3 cm)cos((1.58 rad/s) × (5 s)) = -0.14 cm.4. A pendulum, like the swinging weight under a grandfather clock, can also be an example of simple harmonic motion, but since there's no spring and no spring stiffness the angular frequency is given by a different formula:
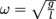 , where l is the length of the pendulum (the mass of the pendulum doesn't matter). How long does a clock pendulum need to be in order to swing once per second?
, where l is the length of the pendulum (the mass of the pendulum doesn't matter). How long does a clock pendulum need to be in order to swing once per second?One swing per second translates to one full cycle every two seconds (tick, tock—back and forth), or a frequency of 0.5 Hz. Half a hertz is equal to an angular frequency of ω = 2πf = 2π × (0.5 Hz) = π rad/s. Therefore we have
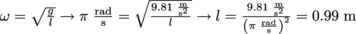 .
.5. A musical note used frequently for tuning instruments is an A, which clocks in at 440 Hz. What is this note's equivalent angular frequency?
ω = 2πf = 2π × (440 Hz) = 2765 rad/s
Waves
1. When you throw a rock into a pond (or a child into a swimming pool, for our more suburban readers), the impact creates ripples that spread outward in a circle. Are these ripples transverse waves or longitudinal?Ripples are transverse waves. They are disturbances in the surface of the water that move in the vertical direction, while the crests themselves spread out from the point of impact horizontally.
2. What is the period of the motion of an LP record that spins at 33.3 rpm?
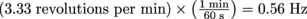 . This is equivalent to rotating with a period of
. This is equivalent to rotating with a period of 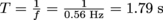 , or one full revolution every 1.79 s.
, or one full revolution every 1.79 s.3. What is the period of a point right next to the center of the record? What about a point on the outside edge of the record? Which point moves faster?
Any point on the record must have the same period (1.79 s), since the entire record rotates with the same frequency. However, a point on the outside edge of the record will have to cover more distance within that time frame, and so will be moving faster than a point in the middle in order to ensure the periods remain identical.
4. All visible light waves move at the same speed (conveniently referred to as the speed of light, or c), where c = 3×108 m/s. How many times faster than red light (650 nm wavelength) does blue light (450 nm wavelength) oscillate?
For light, we can write v = fλ as c = fλ, or
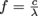 . Then we have
. Then we have 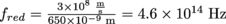 and
and 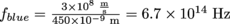 . Based on this, blue light oscillates
. Based on this, blue light oscillates 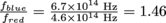 times faster than red.
times faster than red.5. What is the period of a pendulum 1 m in length? (Remember that for a pendulum
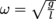 .)
.)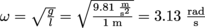 . Therefore, the period is
. Therefore, the period is 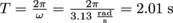 .
.Standing Waves and Interference
1. A standing wave in a 2 m long string has a wavelength of 1 m. How many antinodes does it have, and where are they located?A 1 m wavelength means two complete sine cycles can fit in the 2 m string, so there are four antinodes (one at each local maximum and minimum of the waveform). The maxima and minima occur when
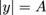 and
and 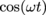 is at its maximum value of 1. In other words, the antinodes are located at the points where
is at its maximum value of 1. In other words, the antinodes are located at the points where 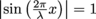 , or
, or 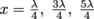 and
and 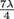 . Since our wave has a wavelength of 1 m, the antinodes will be located 0.25, 0.75, 1.25, and 1.75 m from the beginning of the string.
. Since our wave has a wavelength of 1 m, the antinodes will be located 0.25, 0.75, 1.25, and 1.75 m from the beginning of the string.2. At what time after t = 0 will a standing wave with frequency 60 Hz return to its original shape?
A standing wave will return to its original shape when its cosine term returns to its value at t = 0—that is, when cos(ωt) = 1, or ωt = 2π. Solving for t gives us
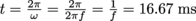 . If this looks familiar, it's because
. If this looks familiar, it's because  is exactly equal to T, the period of a wave—which is defined as the time it takes a wave to complete one entire cycle and return to its original form.
is exactly equal to T, the period of a wave—which is defined as the time it takes a wave to complete one entire cycle and return to its original form.3. What is the resulting wave when these two waves interfere with one another?

Answer:
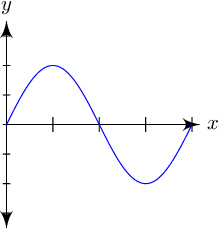
4. A string is shaken such that two traveling waves appear on opposite ends: one,
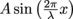 , starts on the left and travels to the right, and another,
, starts on the left and travels to the right, and another, 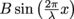 , starts on the right and travels left. What is the wave that results from the two traveling waves interfering with each other? Is it a standing wave?
, starts on the right and travels left. What is the wave that results from the two traveling waves interfering with each other? Is it a standing wave?Since the waves have the same wavelength (and, since they're traveling in the same medium, therefore frequency), we can find the shape of the resulting wave after they interfere by adding the two waves together:
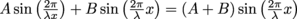 . If and only if A = B, this corresponds to a standing wave of
. If and only if A = B, this corresponds to a standing wave of 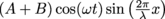 .
.5. The standing waves that arise in pipe organs are a different shape than guitar strings—while a guitar string is pinned on each end so that the endpoints become nodes, making the standing wave look like a sine, the air inside an organ pipe is constrained so that the antinodes are at the endpoints. This makes pipe organ standing waves look like cosines instead of sines, and the formula describing the wave then becomes:
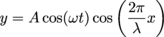
Sketch the wave created in a 1.54 m pipe at time t = 0 when the sound waves resonate with a frequency of 440 Hz. The speed of sound in air is about 340 m/s.
At t = 0, the standing wave equation for the pipe simplifies to
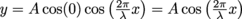 . The relationship between wave speed and frequency gives us our wave's wavelength:
. The relationship between wave speed and frequency gives us our wave's wavelength: 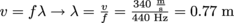 . This wavelength means exactly two cycles of the cosine waveform fit in the pipe.
. This wavelength means exactly two cycles of the cosine waveform fit in the pipe.
The Doppler Effect
1. If an ambulance siren has a nominal frequency of 500 Hz, what frequency will it appear to be as the ambulance drives up behind you at 40 miles per hour (about 17.88 m/s)?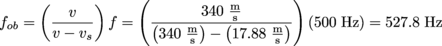
2. What is the wavelength of the observed sound as the ambulance in the previous question drives away from you at the same speed?
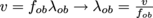 , where
, where 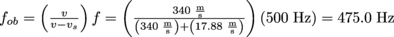 . Then
. Then 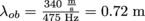 .
.3. Once the ambulance gets to the hospital, it parks—but the siren keeps ringing for a few seconds. If you drive past the hospital, does the siren sound the same to you as to the ambulance driver? If not, as you approach the hospital, how is the siren's frequency shifted?
No, the siren does not sound the same to you as the ambulance driver—even though the observer, and not the source, is moving. A Doppler shift will still happen in this situation, since you driving towards the ambulance is pretty much indistinguishable (mathematically!) from the ambulance driving towards you. That means as you drive towards the stationary siren, it will sound like it has a higher frequency than it actually does.
4. The radar guns wielded by highway patrol officers, that are the bane of any race car driver or Fast and Furious enthusiast, use a technology called Doppler radar. They make use of the Doppler Effect and radio waves (a form of electromagnetic radiation, just like visible light or microwaves) to measure the speed of a moving object.
The radio waves travel at the speed of light (called c, around 3×108 m/s) out of the gun and towards an object moving at speed v, then bounce off and are reflected back towards the gun with a different frequency than when they left. This difference in frequency is proportional to the speed of the moving object, given by
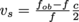 .
.What is the observed frequency when a 30 GHz radar beam is sent at a car traveling towards the police at 40 m/s?
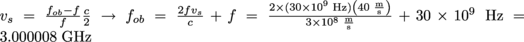
Pretty impressive that gets you a $300 ticket, huh?
5. If both the source of a wave and the observer of the wave are moving, the Doppler Effect still holds, but with one extra term. As an ambulance passes you at speed vs while you're on the road driving at speed vob, the frequency you hear will be
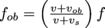 . For our 500 Hz ambulance siren passing you at 17.88 m/s, what will the frequency you hear be if you're driving at 12 m/s?
. For our 500 Hz ambulance siren passing you at 17.88 m/s, what will the frequency you hear be if you're driving at 12 m/s?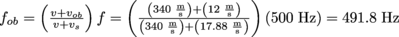 . Because you're moving as well, this frequency is shifted less than in the case of problem 2, where only the ambulance was moving, giving it a greater relative speed.
. Because you're moving as well, this frequency is shifted less than in the case of problem 2, where only the ambulance was moving, giving it a greater relative speed.