Wave Motion
All right, all right. So we've been holding back. You're here to learn about waves, after all. But simple harmonic motion is wave motion: the repeated oscillations of an object away from (and back to!) an equilibrium point. Think block on spring, pendulum on clock, tides on beach, British monarchs on motorcades...the list goes on and on.
Let's imagine you're playing with a yo-yo. You send the yo-yo down, maybe bounce it around a little, and then pull it back up. Rinse and repeat. If we were to graph the height of the yo-yo versus time, it might look like this:
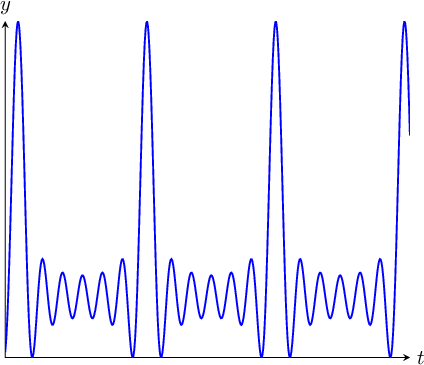
This is wave motion: a pattern that repeats on and on in time. From the last section, we could figure out this wave's cycle, amplitude, phase, and frequency (plus angular frequency), but let's recap—and add one more crucial wave term:
Traveling waves are broken up into longitudinal waves and transverse waves. Most examples of mechanical waves that come to mind are probably transverse traveling waves—they oscillate in a direction perpendicular to the direction which they travel in. An ocean wave that goes up and down as it makes its way toward shore, for example, is a transverse wave. If you'd like to make a transverse wave of your very own, get a piece of string and tie it to a doorknob in your house (or, even better, get a friend, sibling, or particularly adroit and obedient dog to hold the other end). Grab hold of the free end, and give the string one quick shake. You should see a pulse travel down the length of the string.
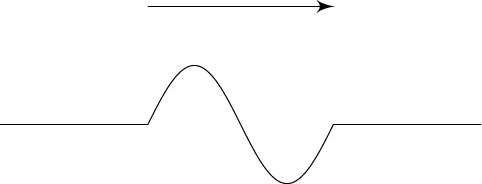
Shake your end more, and you'll make more pulses, which each travel down the string at speed v.
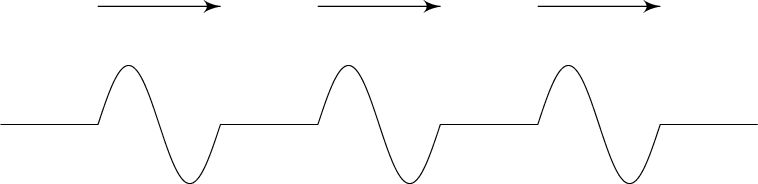
The distance (measured in meters) between these perfectly repeated pulses is called wave's wavelength, λ.
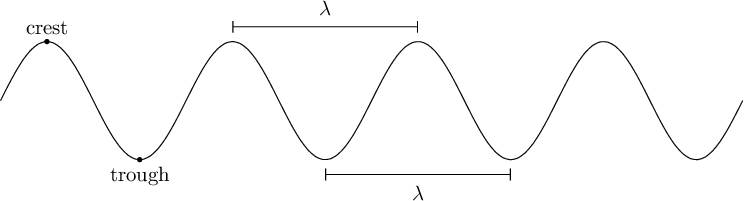
It's often easiest to measure wavelength from the wave's crests (the tallest point of the waveform) on its troughs (the lowest points), but λ will be the same as long as your consistent about where on the cycle you measure from.
Based on wavelength and velocity, we can figure out the wave's frequency without having to use a stopwatch. Think about it this way: a wave travels some distance equal to its wavelength (λ) in a time equal to its period (T). If the wave is traveling at speed v, we know that its speed is its distance traveled divided by the time it takes to travel that distance: . A somewhat more useful way to write this is to realize that
. A somewhat more useful way to write this is to realize that  is the same as f, the wave's frequency:
is the same as f, the wave's frequency:
v = fλ
Transverse waves are not limited to the physical. Light, one of the universe's most prevalent form of wave, is a transverse wave—not a ray or a beam or even a golden drop. As light moves from, say, the sun to Earth, it wiggles up and down in a perfect sinusoid. Different frequencies and wavelengths of this oscillation are responsible for all of light's different colors, and even for different forms of light that physicists call electromagnetic radiation: things like microwaves, radio waves, and, yes, gamma rays, too.
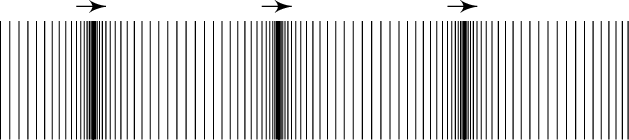
The other kind of traveling wave, a longitudinal wave, moves very differently from a transverse wave. In a longitudinal wave, the direction of oscillation is the same as the direction of motion. This is a little harder to visualize, so hopefully your friend/sibling/dog/doorknob is still nearby. Grab a slinky and give one end to your accomplice. (If you can't find a slinky, well, they look like this, but with better hair.) Stretch the slinky out between you, and give your end a sharp push. You should be able to see the metal coils compress and wiggle their way down the length of the entire slinky:

If you keep pushing the end of the slinky, you'll make many longitudinal pulses, the same way you made a train of transverse pulses by shaking the string.

Longitudinal waves have a wavelength, just like transverse waves—just look for the two points where the amount of compression is the same.
Longitudinal waves are also abundant in nature—the chief example being sound. All sounds are pressure waves moving through the air towards your ears, buffeting air molecules back and forth as the waves move. Higher frequency sound waves are higher pitched: birds chirping, bells ringing, or whistles blowing. Lower frequency sounds sound deeper: drums echoing, foghorns blaring, or (and turn up the subwoofer for this one) sci-fi film alien motherships landing.
Brain Snack
There are a lot of cool waves in the world, but the best ones to watch in slow motion are definitely shockwaves.
Let's imagine you're playing with a yo-yo. You send the yo-yo down, maybe bounce it around a little, and then pull it back up. Rinse and repeat. If we were to graph the height of the yo-yo versus time, it might look like this:

This is wave motion: a pattern that repeats on and on in time. From the last section, we could figure out this wave's cycle, amplitude, phase, and frequency (plus angular frequency), but let's recap—and add one more crucial wave term:
- Cycle. The repeating part of the pattern.

- Amplitude. The difference between equilibrium (your hand) and the lowest point of the yo-yo's movement.

- Phase. How far from zero the wave starts.

- Frequency. How often the wave repeats. This can be converted to angular frequency using the formula ω = 2πf. It's hard to draw frequency on a graph, however, so we often resort to...
- Period. A wave's period (T) is the total length of time, in seconds, it takes the wave to repeat itself. If that sounds familiar, it's because period is the exact opposite of frequency. If a yo-yo bounces 3 times per second (frequency), it takes 1/3 of a second to do each bounce (period). In other words,
 , or
, or  .
. 
Traveling Waves
Objects that follow wave patterns have two choices: they can either move back and forth in one place (imagine jumping rope) or move along a path (think ocean waves crashing into the beach). These two categories are called standing waves and traveling waves. We'll get to standing waves in the next chapter. For now we'll focus on just the travelers.Traveling waves are broken up into longitudinal waves and transverse waves. Most examples of mechanical waves that come to mind are probably transverse traveling waves—they oscillate in a direction perpendicular to the direction which they travel in. An ocean wave that goes up and down as it makes its way toward shore, for example, is a transverse wave. If you'd like to make a transverse wave of your very own, get a piece of string and tie it to a doorknob in your house (or, even better, get a friend, sibling, or particularly adroit and obedient dog to hold the other end). Grab hold of the free end, and give the string one quick shake. You should see a pulse travel down the length of the string.

Shake your end more, and you'll make more pulses, which each travel down the string at speed v.

The distance (measured in meters) between these perfectly repeated pulses is called wave's wavelength, λ.

It's often easiest to measure wavelength from the wave's crests (the tallest point of the waveform) on its troughs (the lowest points), but λ will be the same as long as your consistent about where on the cycle you measure from.
Based on wavelength and velocity, we can figure out the wave's frequency without having to use a stopwatch. Think about it this way: a wave travels some distance equal to its wavelength (λ) in a time equal to its period (T). If the wave is traveling at speed v, we know that its speed is its distance traveled divided by the time it takes to travel that distance:
 . A somewhat more useful way to write this is to realize that
. A somewhat more useful way to write this is to realize that  is the same as f, the wave's frequency:
is the same as f, the wave's frequency:v = fλ
Transverse waves are not limited to the physical. Light, one of the universe's most prevalent form of wave, is a transverse wave—not a ray or a beam or even a golden drop. As light moves from, say, the sun to Earth, it wiggles up and down in a perfect sinusoid. Different frequencies and wavelengths of this oscillation are responsible for all of light's different colors, and even for different forms of light that physicists call electromagnetic radiation: things like microwaves, radio waves, and, yes, gamma rays, too.
The other kind of traveling wave, a longitudinal wave, moves very differently from a transverse wave. In a longitudinal wave, the direction of oscillation is the same as the direction of motion. This is a little harder to visualize, so hopefully your friend/sibling/dog/doorknob is still nearby. Grab a slinky and give one end to your accomplice. (If you can't find a slinky, well, they look like this, but with better hair.) Stretch the slinky out between you, and give your end a sharp push. You should be able to see the metal coils compress and wiggle their way down the length of the entire slinky:

If you keep pushing the end of the slinky, you'll make many longitudinal pulses, the same way you made a train of transverse pulses by shaking the string.

Longitudinal waves have a wavelength, just like transverse waves—just look for the two points where the amount of compression is the same.

Longitudinal waves are also abundant in nature—the chief example being sound. All sounds are pressure waves moving through the air towards your ears, buffeting air molecules back and forth as the waves move. Higher frequency sound waves are higher pitched: birds chirping, bells ringing, or whistles blowing. Lower frequency sounds sound deeper: drums echoing, foghorns blaring, or (and turn up the subwoofer for this one) sci-fi film alien motherships landing.
Brain Snack
There are a lot of cool waves in the world, but the best ones to watch in slow motion are definitely shockwaves.