We already know that series and integrals share some similar properties. We're going to show that, by replacing the series with an equivalent integral, we can determine if the series converges.
In terms of our Pandora's box, we're just replacing our grilled cheese with something else. Assume we've replaced them with gremlins. Maybe we should keep the box shut on these guys.
Now, we're going to test the convergence or divergence of some series by doing some reasoning similar to what we did when studying left-hand and right-hand sums for integrals.
Integral Test: Let f be a non-negative decreasing function on [c, ∞) where c is an integer. If the integral

converges, then the series

converges.
If the integral diverges, then the series also diverges.
Like we mentioned before, the integral test replaces grilled cheese with gremlins. They're hard to tame, but if you can do so, you can open the box safely. If you can't tame the gremlins, then keep that box shut.
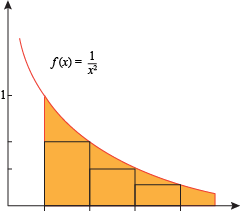
The integral test works because, depending on how we draw the series, we can choose whether the rectangles will cover more or less area than the integral.
In the example with the harmonic series we drew the series as an overestimate. Since the integral diverged, we knew the series had to diverge.
If we have an integral that converges, we draw the series as an underestimate (right-hand sum) instead. Since a convergent integral describes a finite area, the smaller area covered by the rectangles must also be finite.
Example 1
Does the constant series
where a > 0, converge or diverge? |
Example 2
Does the harmonic series
converge or diverge? |
Example 3
Does the series
converge or diverge? |
Example 4
If possible, use the integral test to determine whether the series
converges or diverges. |
Example 5
If possible, use the integral test to determine whether the series Σ sin n converges or diverges. |
Exercise 1
If the terms of a series approach zero, must the series converge? Justify or provide a counterexample.
Exercise 2
Does

converge or diverge?
Exercise 3
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

Exercise 4
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

Exercise 5
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

Exercise 6
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.

Exercise 7
For the series, determine if it's okay to use the integral test. If so, use the integral test to determine whether the series converges or diverges.








 passes through all the dots.
passes through all the dots.




 is decreasing, a left-hand sum is an overestimate . An overestimate of an infinite value is infinite, so
is decreasing, a left-hand sum is an overestimate . An overestimate of an infinite value is infinite, so

 is non-negative and decreasing on [1,∞) we can use the integral test. The integral
is non-negative and decreasing on [1,∞) we can use the integral test. The integral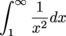
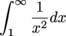
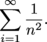



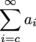
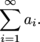








 . This function is decreasing and non-negative on [1,∞), and the nth term of the series is f(n).
. This function is decreasing and non-negative on [1,∞), and the nth term of the series is f(n).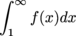
 is less than 1), the series must also diverge.
is less than 1), the series must also diverge.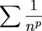







 as x goes to infinity:
as x goes to infinity:
