TNReady Integrated Math III

Caught a case of Integrated Math classes you can't seem to kick? Are you plagued by lessons on reasoning with units, creating functions, and solving equations? Symptoms of TNReady's Integrated Math III include modeling periodic behaviors such as using trigonometric functions, rationalizing away your friends' equations, and spontaneously generating extraneous solutions to radical functions. Whether you're coughing up formulas or running a fever of 360° circles, Shmoop is here to cure the end of the end-of-course blues by aligning you with the normal bell curve.

This course, constructed with the help of some protractors and compasses, is fully equipped with brand new computer-based question types making it both infectious and contagious.

What's Inside Shmoop's Online TNReady Integrated Math III Prep

Shmoop is a labor of love from folks who are really, really into learning. Our test prep resources will help you prepare for exams with comprehensive, engaging, and frankly hilarious materials that bring the test to life. No, not like that. Put down those torches.

Here, you'll find…

• an in-depth review of every topic covered on the test
• a full arsenal of practice problems 
• a diagnostic exam to see what you know
• a full-length practice assessment
• secret tips and strategies from people who know things
• chances to earn Shmoints and climb the leaderboard

Sample Content

Given two endpoints, the midpoint formula tells us the point that's an equal distance between the two. In geometry, we could use this to find a point half way up a triangle.

Of course, at this age it's no longer a secret that life isn't always fair. Not everybody gets to meet in the middle—in life or geometry. We can determine a point P that partitions a line segment in the ratio m:n using the following formula.

Say two dueling mathematicians decide to meet on neutral ground between their two offices. An ongoing feud between triangles and circles is about to be settled once and for all, but sadly the midpoint is home to Professor Cubit, who wants nothing to do with the whole situation.

(Yes, we're aware this is less exciting than two dueling magicians, but at least nobody's going to disappear or turn into a frog.)

Dr. C. Ircle is at (5, -4), which we'll call point 1, and Professor T. Riangle is located at (-1, 8), point 2. If we'd like the ratio that separates the segment to be 3:4 from point 1 to 2, plug the numbers into the formula. Make sure to keep the points 1 and 2 in the right order as set by the ratio. The coordinates of Dr. C. Ircle's location should come before those of Professor T. Riangle's location.

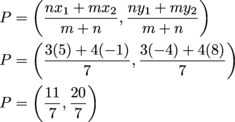
With all the math knowledge those guys have, we're sure they can measure that to the nearest inch before they begin their quarrel. Neutral point P has been found and hopefully the age-old debate finally comes to an end.