ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
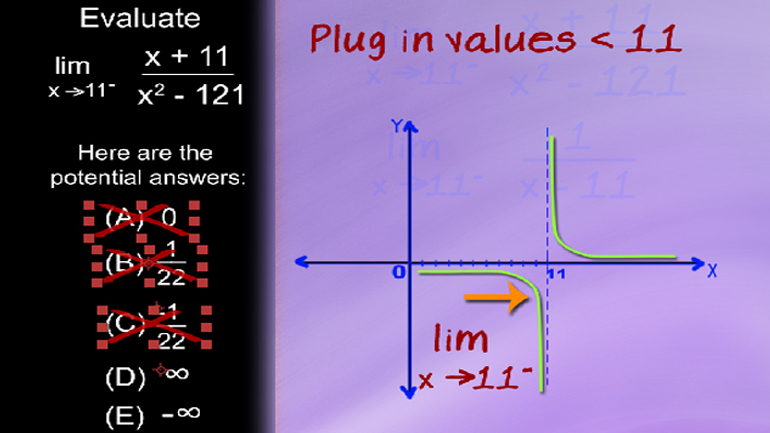
AP Calculus 2.3 Limits 222 Views
Share It!
Description:
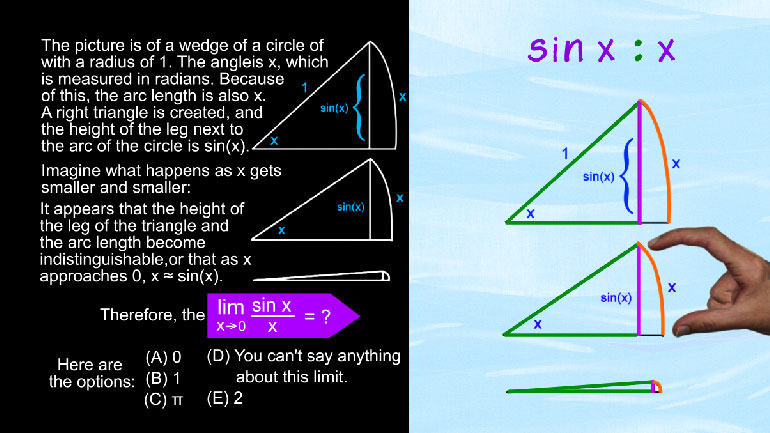
AP Calculus 2.3 Limits. Which of the following facts is helpful in determining the limit?
Transcript
- 00:00
Thank you We sneak here's your smoke too Sure brought
- 00:05
to you by sine x If you're having signed x
- 00:09
problems we recommend suiting All right which of the following
- 00:15
facts is helpful in determining the limit of sine x
- 00:18
over acts as x approaches npr All right And here
Full Transcript
- 00:23
the potential answers This is it Okay so we've got
- 00:28
one of those choose the right roman numerals questions In
- 00:34
this case we're trying to see which one of these
- 00:36
facts helps us determine the limit Ok so let's go
- 00:39
through each option and pick out the ones that are
- 00:41
true Roman numeral one negative one over acts is less
- 00:45
than or equal to sign of acts over x is
- 00:48
also less than or equal to one over x Well
- 00:52
when we deal with trying to find limits have founded
- 00:54
trig functions like this we know instantly it's a job
- 00:58
for the squeezing serum dresses It works much better with
- 01:01
functions that goes with it squeezing terms as if the
- 01:04
output of a function f of acts is always between
- 01:07
the outputs of two other functions g of axe and
- 01:10
h of x and g of axe and h of
- 01:13
x both approached the lind l as x approaches infinity
- 01:17
then the function half of acts also obstruct his scalp
- 01:21
as x approaches infinity Okay so we know from the
- 01:25
basic during function graph sign of acts that the y
- 01:27
values of sine x are limited betweennegative one and one
- 01:30
in other words sign effects is unfounded So if we
- 01:34
just divide the entire inequality by Acts we'd get negative
- 01:37
1 over acts It is less than or equal to
- 01:40
sign x over x which is last center equal to
- 01:42
one over x This will definitely help us find the
- 01:46
limit The boom roman numeral one is correct and we
- 01:49
can cross off answers Be seeing me because well they
- 01:51
include one group Now we just have to check to
- 01:54
see if roman numeral two is correct Since there's no
- 01:57
answer Choice with options One two three All being through
- 02:00
the next step in applying squeezing term is to actually
- 02:03
find the limits His ex approaches infinity of each of
- 02:05
the parts of the inequality The negative one over accident
- 02:08
signed x over act and the one over act which
- 02:12
means we just have to know the limit of one
- 02:14
overnegative acts and won over axes X approaches infinity For
- 02:18
that we have statement too statement to tells us that
- 02:21
the limit of one over axes x approaches is zero
- 02:24
Perfect Of course we still need to know the limit
- 02:27
of negative one over access x approaches infinity to solve
- 02:30
the limit as x approaches Infinity of sine x overact
- 02:34
bye Statements one into both Tell during the limit Statement 00:02:39.23 --> [endTime] from him to our true Our answers Yeah
Up Next
AP Calculus: Problem Explanation Limits Drill 1, Problem 1. Which of the following are true about the pictured function?
Related Videos
AP Calculus: AB/BC Limits Drill 1, Problem 5. Evaluate the limit.
Breathe in deeply through the nose... Now slowly exhale... Breathe in... And out... Now visualize the graph of the limit of f(x) as x approaches 2....
AP Calculus 1.4 Limits. Given the limit, which of the following are true?