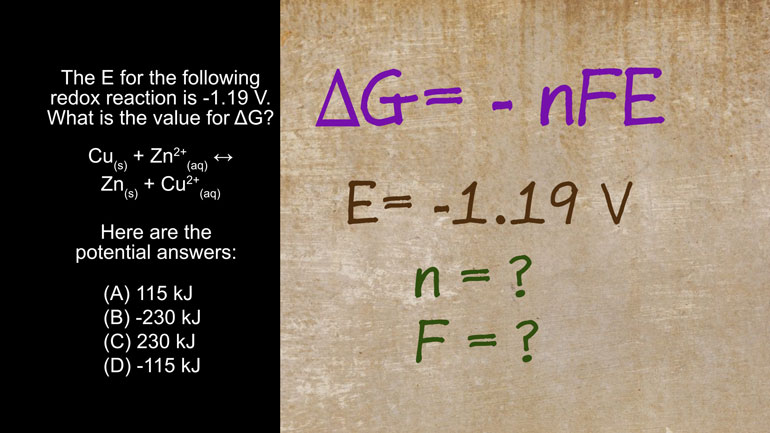AP Chemistry 3.5 Structure and Arrangement of Atoms

Let's start at the top with (A).

(A) just means that all the stuff in a solid is in a very small space.

Does that seem true?

Well, if you’ve ever vaporized anything in the microwave, let’s say a grape, you [A microwave and a bunch of grapes appear]

probably know that if you put a solid object in and heat it to make a gas or a plasma,

it will often expand to fill the microwave. [Microwave explodes and grapes hit a man in the face]

Not that…we've tried this before….ahem.

Anyway, it seems like A might be a reasonable choice, so we'll come back to it. [Car drives down a road]

The next answer says that solids have the highest average kinetic energy relative to

liquids and gases.

Average kinetic energy is what temperature measures. [Thermometer gauge rising]

A high temperature means a high average kinetic energy, and a low temperature means a low

average kinetic energy.

This means the question is actually asking us if solids are generally hotter than liquids [A log of wood, rain and gas]

and gases.

Although having gas is not hot when you’re on a date, gases themselves are the hottest [Man farts walking through a park with a girl]

state of matter on average.

Temperature-wise.

We don’t know how they fare in online dating… [Mobile phone with a Tinder picture of a gas]

Solids are colder than both liquids and gases in fact, so we can cross off choice B right away.

Let’s move on to answer C, which says that the particles are in a randomly assorted 3D

structure, brought to you by Oculus [An oculus rift AI headset]

As much as your Lego kit at home may be in disarray, the atoms within each Lego piece [Boy surrounded by lego pieces]

should be arranged fairly regularly compared to a liquid or a gas….unless you’ve run

your Legos through a particle accelerator. [Pieces of lego shooting through a particle accelerator]

Maybe you have, maybe you haven’t.

…Don't try that at home either.

So answer C is off the table.

Moving on to answer D. [Car drives past a sign labelled 'D']

This next statement says that solids have a definite volume from an indefinite shape.

If you take a sugar cube as an example, you can see that a solid has a very definite volume

as well as a definite shape. [A sugar cube in a kitchen]

if you pound the cube into dust, it still has a definite shape. [Hammer smashes sugar cube to dust]

It’s just gone from a cube to an amorphous pile of dust that has no geometric name.

So answer D is off the table because indefinite shape does not describe solids.

That leaves us with our original answer A, that solids constitute a condensed state of

matter.

So it looks like nothing was the matter with answer A… [Guys cheering in a pub]

…We'll see ourselves out.