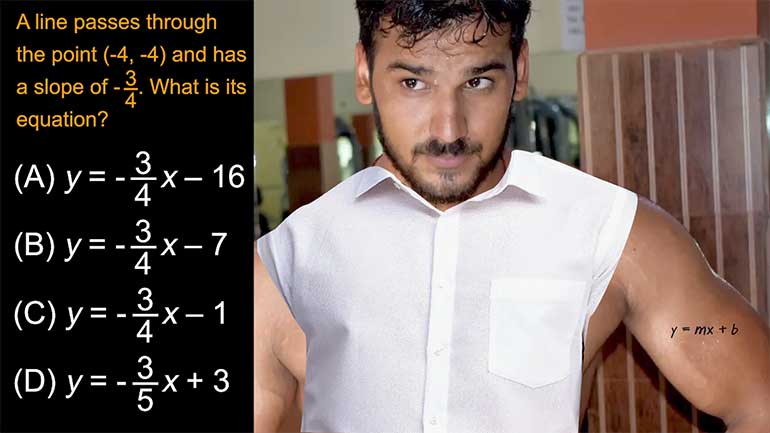ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Simplifying Rational Expressions 1406 Views
Share It!
Description:
Rational expressions are too complex... it's about time someone simplified them.
- Mathematics and Statistics Assessment / Rational and Exponential Expressions, Equations, and Functions
- Algebra / Rewrite rational expressions
- Algebra / Rewrite rational expressions
- Algebra / Write expressions in equivalent forms to solve problems
- Algebra / Write expressions in equivalent forms to solve problems
- Algebra / Write expressions in equivalent forms to solve problems
Transcript
- 00:04
Simplifying Rational Expressions, a la Shmoop.
- 00:07
Sam is beginning his college career, and has just joined the fraternity Alpha Delta Nerda.
- 00:14
School policy says that no physical hazing is allowed...
- 00:17
...so Alpha Delta Nerda does its own kind of hazing...
- 00:20
...and makes the guys solve math problems to figure out what
Full Transcript
- 00:23
their "special number" will be for the rest of the year.
- 00:28
Sam gets an anonymous letter under his door that says,
- 00:31
Simplify 36 minus 3p all over 4p minus 48.
- 00:37
To start, let's take a look at the numerator to see if we can factor out anything.
- 00:41
We see that 3 is the greatest common factor of 36 and 3p,
- 00:45
3 goes into 36 twelve times and 3 goes into 3 one time...
- 00:50
...so 36 minus 3p becomes 3 times 12 minus p.
- 00:55
We can see that in the denominator the greatest common factor is 4.
- 00:59
4 goes into 4 one time and goes into 48 twelve times...
- 01:03
...so we can factor out the 4 to get 4 times p minus 12.
- 01:07
12 minus p is the same as p minus 12... when multiplied by a negative.
- 01:13
So we can pull out a negative 1 from the top...
- 01:18
to get negative 3 times p minus 12, over 4 times p minus 12.
- 01:27
The top and bottom of the expression have common factors of p minus 12,
- 01:32
so we can just cancel these out.
- 01:33
And we're left with negative three-fourths!
- 01:37
That's it! Sam's special number is negative three-fourths!
- 01:40
He has so got this college thing in the bag.
Up Next
Mosquitos need their caffeine, just like the rest of us. Wouldn't think zipping around and stinging people all day long sap your energy?
Related Videos
What is the equation of the line graphed above?
A line passes through the point (-4, -4) and has a slope of . What is its equation?
Line A has an x-intercept of -4 and a y-intercept of 8. What is its slope?