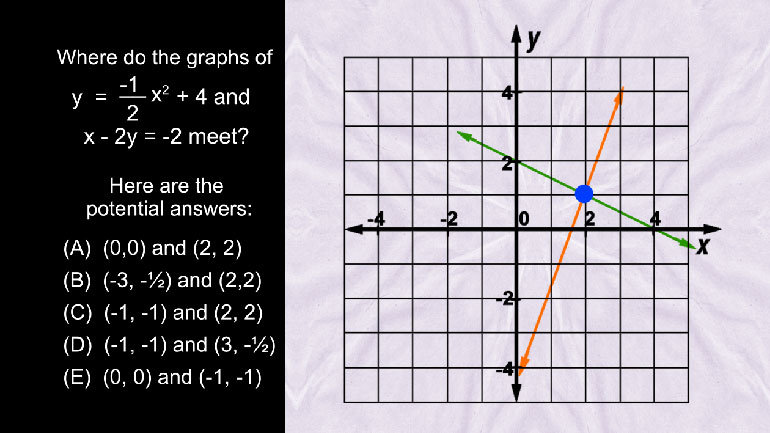
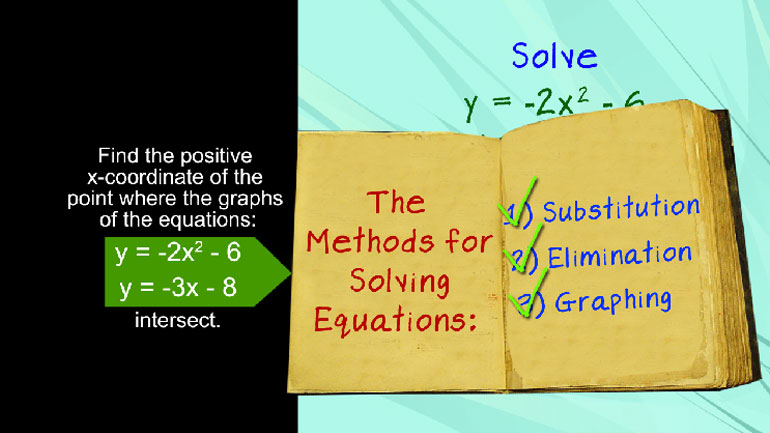
ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Solving Quadratic Equations: Completing the Squares 4313 Views
Share It!
Description:
Why “quadratic?” Is 4 its lucky number? Or does it just spend a lot of time at the gym?
Transcript
- 00:04
Solving Quadratic Equations: Completing the Square, a la Shmoop.
- 00:09
A new park in town is being funded by a conglomerate of handkerchief makers. [Man sneezes and a woman hands him a handkerchief]
- 00:14
They've named the park Pocket Square.
- 00:16
But they are having trouble completing the square, so they call... ['Pocket Square' sign drops into the park]
- 00:21
…The QuadSquad In order to complete the square, the QuadSquad ['The QuadSquad' car arrives]
Full Transcript
- 00:25
has to solve this problem:
- 00:27
Two-x-squared plus five-x minus 42 equals zero. [Man stood in a hard hat next to a blu print sheet]
- 00:33
Okay to solve first, add forty-two to both sides to get...
- 00:39
…two-x-squared plus eight-x equals 42.
- 00:42
Divide every term by two so that the number before the x-squared is 1.
- 00:47
…x-squared plus four-x equals twenty-one.
- 00:51
It's time to complete the square. [Woman holding the equation on a sheet waiting expectantly]
- 00:53
We want to add a number to the left side such that it becomes a perfect square.
- 00:59
We can find this number by taking the coefficient of the x-term, dividing it by 2, and squaring
- 01:06
it.
- 01:07
In this case, our coefficient of the x term is 4.
- 01:11
4 divided by 2 equals 2.
- 01:15
Two-squared equals 4.
- 01:17
Eureka!
- 01:18
We've found the number that completes the square. [The answer is highlighted]
- 01:22
Whatever we do to one side, we have to do to the other.
- 01:26
So we add 4 to both sides, which gets us x squared plus 4x plus 4 equals 21 plus 4.
- 01:34
Now we can factor the left side of the equation. [The left side is highlighted]
- 01:38
X-squared plus four-x plus four can be simplified to x plus 2 in parentheses squared.
- 01:44
To simplify the right-hand side, we add 21 and 4 to get 25. [The right hand side is highlighted]
- 01:50
All that's left is to take the square root of both sides. [Both sides have a square root sign drawn over them]
- 01:54
Don't forget that the square root can be positive or negative. [Finger appears with piece of knotted string attached]
- 01:57
We're left with x plus 2 equals plus-or-minus the square-root of 25, or just 5.
- 02:04
Subtract two from both sides...
- 02:06
and we get two answers.
- 02:08
x equals either negative 2 plus 5..
- 02:11
…or negative 2 minus 5.. which gives us 3 and negative 7.
- 02:18
And there you have it! [Man in the hard hat points to the answer]
- 02:19
The equation for the square is complete.
- 02:21
And Pocket Square is complete as well. [The QuadSquad car reverses away]