ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
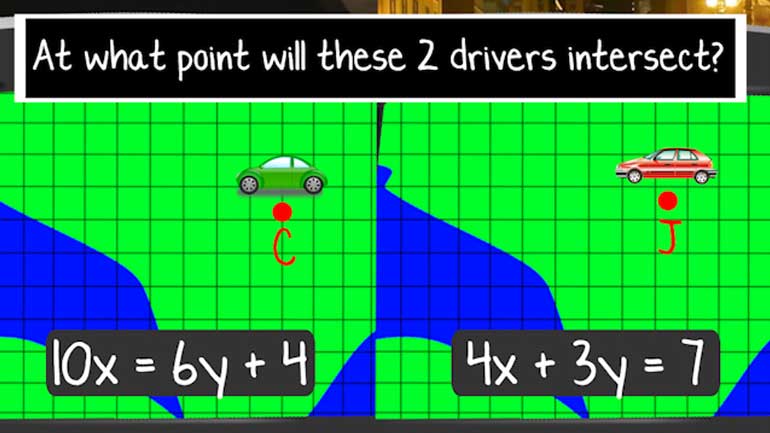
Solving Systems of Equations by Graphing 16954 Views
Share It!
Description:
To solve systems of equations by graphing, just simplify the equations to be in slope intercept form (y = mx + b), and then graph them. Finally, find the intersection point... and you have your variable values. Easy... right?
Transcript
- 00:04
Solving Systems by Graphing a la Shmoop. The mayor of New Chunk City has banned all
- 00:13
sugary beverages larger than sixty-four ounces.
- 00:19
You've heard from a friend that Black's Market is selling sixty-four ounce sodas in the alleyway
- 00:24
behind the store.
- 00:27
Unfortunately, you don't know where Black's Market is, and all you have are a couple of
Full Transcript
- 00:33
cryptic equations leading the way there.
- 00:36
Graph the equations, and they'll provide you with the coordinates to sugar overload.
- 00:40
Here's the scrap of paper your friend gave you.
- 00:45
We'll tackle the equations by changing them to slope-intercept form first...
- 00:50
Let's start with the top equation...
- 00:52
negative-three-x plus y equals six. You can do this one without sugar and caffeine
- 00:57
coursing through your veins.
- 00:59
Just add three-x to both sides. Doing that, we see that y equals three-x plus six.
- 01:05
The second one is slightly trickier. But if you can mix Coke and Pepsi until it tastes
- 01:09
like Dr. Pepper, this is nothing.
- 01:11
First, subtract x from both sides, giving us two-y equals negative x minus 2.
- 01:19
Then just divide all the terms by two.
- 01:21
We end up with y equals negative one-half x minus 1.
- 01:26
Now we just have to graph them.
- 01:29
We'll do the first equation in blue.
- 01:33
The y-intercept is 6, so we can plot a point at zero-six, which is six up the y-axis.
- 01:40
Because we know slope is rise over run, for every one we run or move to the right along
- 01:45
the x axis, we rise, or move three up the y-axis.
- 01:49
Reversing this, we move three spaces down the y-axis for every one we move left along
- 01:55
the x-axis.
- 01:57
The blue line will intersect the x-axis at negative-two, zero.
- 02:02
We'll do the second equation in red.
- 02:04
The y-intercept is negative 1, so we can plot a point at zero, negative-one on the y-axis.
- 02:11
For every one we run, or move right along the x-axis, we'll move one-half down.
- 02:17
Flipping that, we'll move 1/2 up for every one we move left along the x-axis.
- 02:21
This line, too, intersects the x-axis at negative-two, zero.
- 02:29
So that's where the Black's Market is.
- 02:32
At (-2, 0).
- 02:34
You may have to take the subway there, but we're pretty sure you'll be able to run back
- 02:37
home on a pure sugar rush.
Up Next
How do you solve a system of linear inequalities? Aw, man...and we thought solving a problem like Maria was tough...
Related Videos
Please note: If starting your own petting zoo, Shmoop recommends you stock it with animals that aren’t quite so likely to bite your hand off. Tha...
Solving systems of equations by elimination: Survivor-style. Sorry, y... the tribe as spoken.
ACT Math: Intermediate Algebra Drill 3, Problem 4. Solve this system.