ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Solving Trigonometric Equations 3748 Views
Share It!
Description:
FYI: cats don't like to get wet. Okay, so that fact won't be relevant every time you solve trig equations, but it happens to be this time.
- Functions / Extend the domain of trigonometric functions using the unit circle
- Functions / Model periodic phenomena with trigonometric functions
- Functions / Prove and apply trigonometric identities
- Geometry / Similarity, right triangles, trigonometry, and dimensions
- Geometry / Define trigonometric ratios and solve problems involving right triangles
- Functions / Extend the domain of trigonometric functions using the unit circle
- Functions / Model periodic phenomena with trigonometric functions
- Functions / Prove and apply trigonometric identities
- Similarity, Right Triangles, and Trigonometry / Define trigonometric ratios and solve right triangle problems
Transcript
- 00:00
Thank you We sneak in solving trigonometry equations Allah shmoop
- 00:08
calico is in a precarious situation She naively volunteered to
- 00:12
sit in the dunking booth at a carnival Helped raise
- 00:14
money for the vet club at school Calico is doomed
- 00:17
to her kool aid dunk If the next person in
Full Transcript
- 00:20
line doesn't quickly and correctly solve the following trigon a
- 00:23
metric equations tangent squared of x minus three equals zero
- 00:29
For the interval zero is less than are equal to
- 00:32
x is less than or equal to to pi As
- 00:36
fate would have it speed of the slowest dog in
- 00:38
town is in line to try to solve her question
- 00:40
he grabs the marker and begin solving the equation by
- 00:43
factoring the expression If we factor the expression tangents squared
- 00:47
of x minus three like the difference of two squares
- 00:50
will have the expression the quantity tangent of x minus
- 00:54
square root of three times the quantity tangent of ax
- 00:56
plus square root of three In a bold move he
- 00:59
is now setting each of the quantities equal to zero
- 01:02
He knows that if their product together is zero then
- 01:05
one or both of them must be equal to zero
- 01:08
Solving each of the equations with a speed we frankly
- 01:10
didn't think possible for him He ends up with two
- 01:13
equations using a technique he must have studied with his
- 01:17
trigonometry teacher He is taking the inverse tangent of both
- 01:21
of the equations to solve for x reaching far back
- 01:24
into the recesses of his canine brain He recalls that
- 01:27
the inverse tangent of route three is pi over three
- 01:31
And the inverse tangent of negative Ruth 3 is 2
- 01:34
pi over three Speedy realizes that we've found two answers
- 01:38
within an interval of pie because both pie over three
- 01:42
and two pi over three are less than pie That
- 01:45
makes sense because the tangent function has a period of
- 01:48
pi which means it goes through one full cycle for
- 01:50
every pie radiance Since speedy is looking for all answered
- 01:54
between zero and two pie he has to consider the
- 01:57
answer's between pi and two pi Also in order to
- 02:00
find those values he needs tto add pie each of
- 02:03
the answers he already has So who had pi tau
- 02:07
pi over three We must first make sure both numbers
- 02:10
have the same denominator We can multiply three over three
- 02:13
And a pie to make it have the common denominator
- 02:16
of three When adding fractions we add across the top
- 02:20
and keep the denominator the same so three pi over
- 02:23
three plus pie over three equals four pi over three
- 02:28
brad pie to two pi over three We again have
- 02:31
to make sure both numbers are under the same denominator
- 02:34
we can again multiply three over three two pie to
- 02:36
get three pi over three plus two by over three
- 02:39
adding across the top Numbers we get 3 pie plus
- 02:43
two pi equals five pie over three Those final answers
- 02:48
are x equals pi over three four pi over three
- 02:53
two pi over three and five pie over three Unbelievable
- 02:57
speedy has solved the trig equation Unfortunately the dunk tank
- 03:02
malfunctions and calico gets drenched anyway Sh
Up Next
How do you solve a system of linear inequalities? Aw, man...and we thought solving a problem like Maria was tough...
Related Videos
Please note: If starting your own petting zoo, Shmoop recommends you stock it with animals that aren’t quite so likely to bite your hand off. Tha...
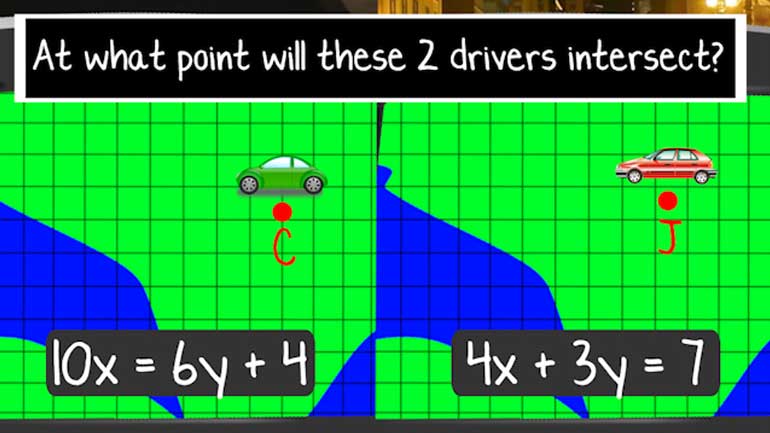
Solving systems of equations by elimination: Survivor-style. Sorry, y... the tribe as spoken.
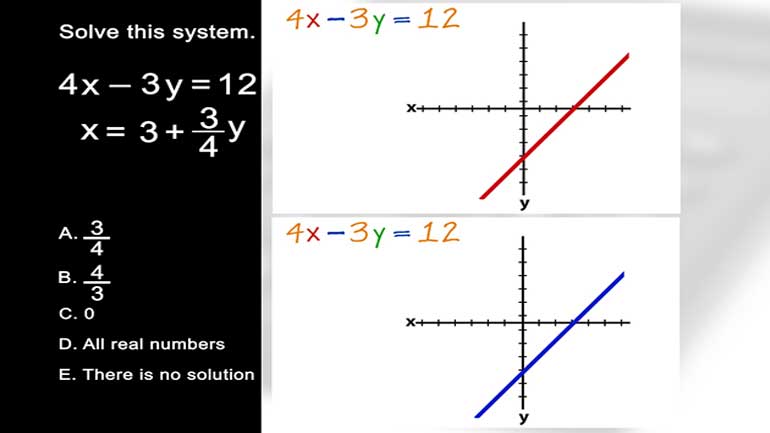
ACT Math: Intermediate Algebra Drill 3, Problem 4. Solve this system.