ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
TSI Math: Predicting a Sequence of Probabilities 58 Views
Share It!
Description:
A standard deck of playing cards contains 4 different suits, each of which has 13 cards. Assuming the deck is shuffled, what is the probability of randomly drawing 2 cards of the same suit in a row?
- Data Analysis, Statistics, and Probability / Probabilistic Reasoning
- Data Analysis, Statistics, and Probability / Probabilistic Reasoning
- TSI Math / Data Analysis, Statistics, and Probability
- Test Prep / TSI
- TSI Mathematics / Data Analysis, Statistics, and Probability
- TSI / TSI Math
- TSI / TSI Mathematics
- Test Prep / TSI
Transcript
- 00:02
Okay sy mash members get a whole new section on
- 00:04
probability or probabilistic reasoning So let's dive in here to
- 00:08
a deck of cards A standard deck playing cards contains
- 00:11
four different suits each of which has thirteen cards Assuming
- 00:14
the deck is shuffled what is the probability of randomly
Full Transcript
- 00:17
drawing two cards of the same suit in a row
- 00:24
Think of these problems with probability in cards as a
- 00:28
simpler form of poker Before we draw the first card
- 00:31
there are a total of four times thirteen or fifty
- 00:33
two cards in the deck We don't know what the
- 00:36
same suit is until after we draw the first card
- 00:39
so it doesn't matter what the first card is right
- 00:41
The first card makes no contribution to the probability Suppose
- 00:44
first card we draw is a heart Well it could
- 00:47
be any suit but we'll use hearts Is an example
- 00:49
here because we're naturally loving people Hear it Some upright
- 00:52
we hard hearts Well we took a heart out of
- 00:54
the deck So now there are only twelve hearts left
- 00:58
in the deck right One goes away and there's only
- 01:01
fifty one cards in the whole deck The probability that
- 01:04
our second card is a heart that is twelve over
- 01:07
fifty one or twenty four percent not twenty five And
- 01:10
this is huge is a huge concept You have to
- 01:13
know this because it'll be on the test We can
- 01:15
almost promise you this concept but as you take away
- 01:17
cards your probabilities change All right Because the first card
- 01:21
could be anything while the probability of randomly drawing two
- 01:24
cards of the same suit in a row is twenty
- 01:26
four percent Another way to arrive at same answer it's
- 01:29
to consider each suit separately For example the probability of
- 01:32
randomly drawing two hearts in a row is thirteen over
- 01:35
fifty two times twelve over fifty one Well this probability
- 01:39
is the same Each of the other three suits we
- 01:42
don't care which suit the cards are as long as
- 01:44
it's the same So add up the individual probabilities for
- 01:48
each suit and you get this mess of a thing
- 01:50
here thirteen or fit to tone The this thing right
- 01:53
there four times that quantity because thirteen over fifty two
- 01:58
equals twelve over fifty one is point two for justice
- 02:02
before it's kind of like we did a little proof
- 02:03
there anyway right answer gets d it's twenty four percent 00:02:07.44 --> [endTime] Them's The odds
Up Next
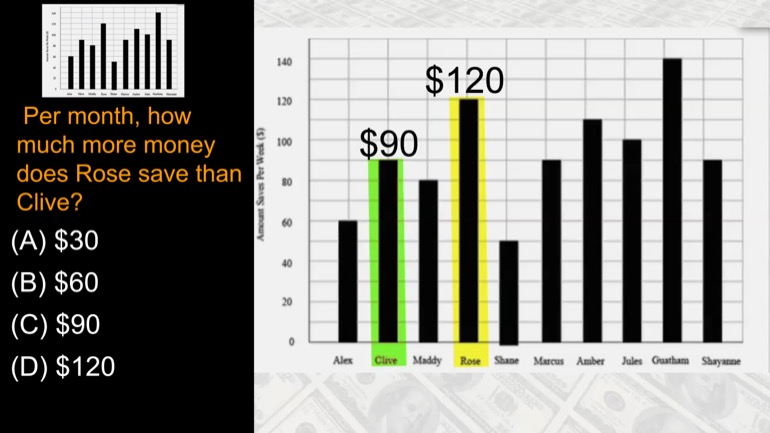
Per month, how much more money does Rose save than Olive?
Related Videos
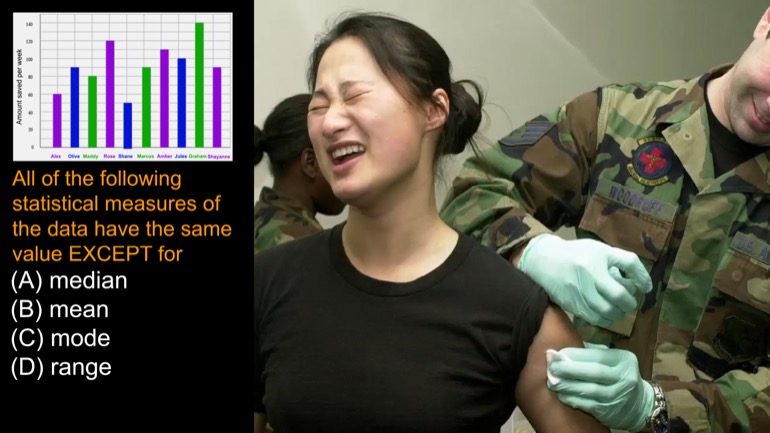
All of the following statistical measures of the data above have the same value EXCEPT for
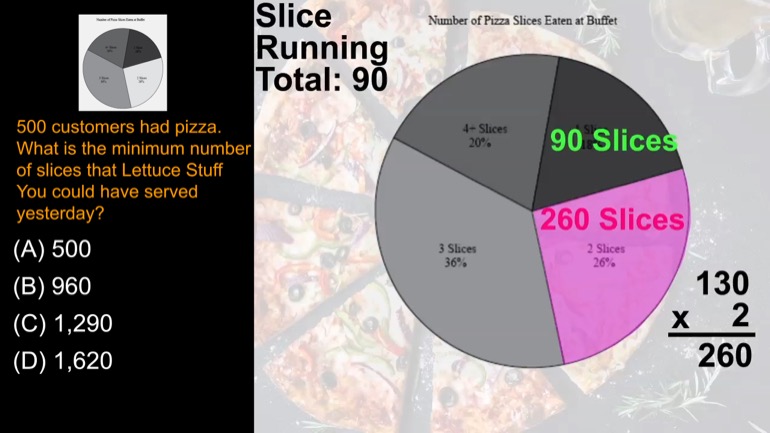
500 customers had pizza. What is the minimum number of slices that Lettuce Stuff You could have served yesterday?
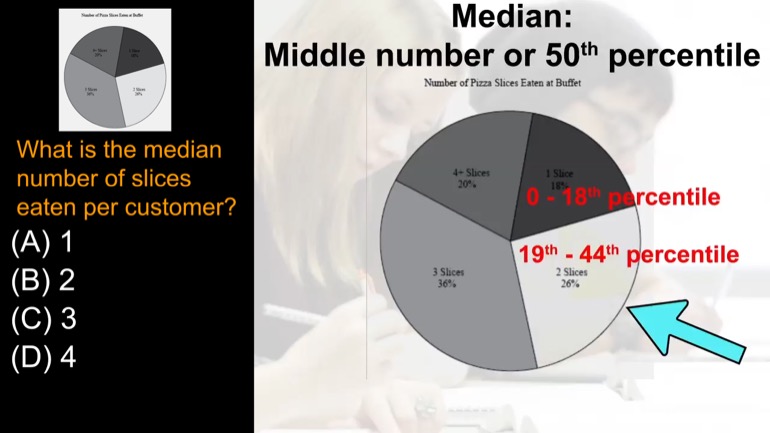
What is the median number of slices eaten per customer?
The following table shows the coffee preferences of everyone in Isabelle's office. What percentage of Isabelle's coworkers put cream in their coffee?