ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
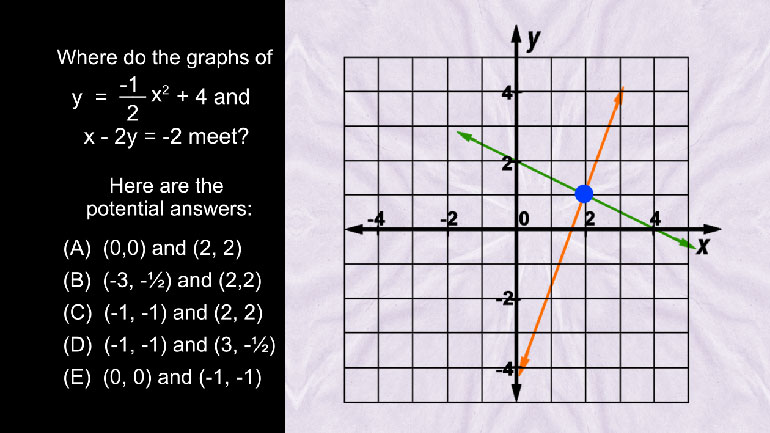
Using the Discriminant 9120 Views
Share It!
Description:
The discriminant is part of the quadratic formula, but that doesn't mean it isn't important in its own right; in fact, once it even guest-hosted The Tonight Show . The discriminant determines the number of solutions in an quadratic formula. If the discriminant is positive, there are two solutions. If the discriminant is zero, there will be one real solution. If it is negative, there will be no real solutions.
Transcript
- 00:04
Using the Discriminant, a la Shmoop. It's never okay to discriminate…
- 00:10
…but you can definitely use the discriminant to help answer some of life's most difficult
- 00:15
questions. In the quadratic formula b2 – 4ac is the
- 00:20
discriminant.
- 00:23
The discriminant determines the nature and number of solutions of a quadratic equation.
Full Transcript
- 00:28
If b2 – 4ac is positive and greater than zero, there will be two distinct, real solutions.
- 00:38
If b2 – 4ac is zero, there will be one distinct, real solution.
- 00:45
But, if b2 – 4ac is negative and less than zero, there are no real solutions.
- 00:56
None. Don't even try to make one up. It won't happen.
- 01:00
Let's get quadratic for a couple of examples.
- 01:08
Our first example is x-squared plus three-x plus five equals zero.
- 01:14
Plugging these bad boys into the discriminant, b squared minus 4ac, we get three-squared
- 01:20
minus four-times-one-times-five.
- 01:23
This simplifies to nine minus twenty, which is negative eleven.
- 01:28
This is less than zero…there are no real solutions.
- 01:33
What does “no real solutions” mean? If we take a look at the graph, the parabola
- 01:37
does not touch the x-axis at any x-value.
- 01:50
For our second example, we have the equation...
- 01:53
x-squared minus six-x minus ten equals zero.
- 01:57
Plugging this into the discriminant it looks like...
- 02:00
six-squared minus four time negative-ten times one.
- 02:05
This is thirty-six plus forty, which is seventy-six.
- 02:09
Seventy-six is greater than zero. So there are two distinct, real solutions to this problem.
- 02:16
By looking at the graph, we can see that there are two real solutions because the parabola
- 02:21
touches the x-axis at two distinct x-values. Okay, so the Magic Discriminant Ball might
- 02:28
not be able to help you with some of life's biggest questions…
- 02:32
… but using the discriminant can help you ace your next math test.