ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
AP Calculus 1.3 Derivatives 241 Views
Share It!
Description:
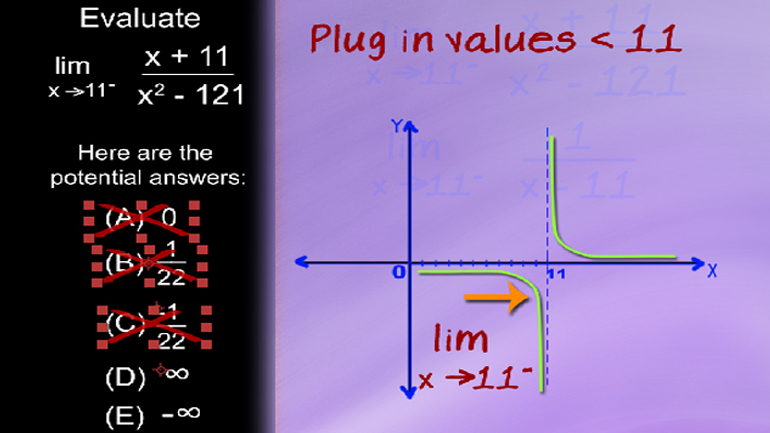
AP Calculus 1.3 Derivatives. Compute the limit.
Transcript
- 00:00
Thank you We sneak and here's your shmoop to shore
- 00:05
Brought to you by brick walls wherever you find one
- 00:09
There's probably a stand up comedian nearby All right compute
- 00:13
the limit of this ugly beast you see right here
- 00:16
All right And here the potential answers thinking thinking uh
Full Transcript
- 00:22
all right If we were to rush headlong into this
- 00:24
problem we bash our heads into a brick wall instead
- 00:27
we should try and simplify it First recall that the
- 00:30
formal definition of a derivative is equal to the limit
- 00:34
as x approaches Si of f of x minus f
- 00:38
of c all over the quantity x minus c look
- 00:42
similar to this problem Yeah fx And this problem is
- 00:45
just even the coastline x This problem is merely a
- 00:48
fancy way of asking for the derivative of the to
- 00:51
the coastline of access acts approaches a now that that's
- 00:54
sorted out we just have to take the derivative of
- 00:56
the to the co sign of a to find the
- 00:58
answer Remember that the derivative of k to the power
- 01:01
of axe is equal to k to the power of
- 01:03
axe times the natural laws of k using that formula
- 01:07
For this case we get e to the power of
- 01:09
co sign a times the natural log of e since
- 01:13
we're studious test takers we won't forget the chain rule
- 01:16
number That one general means that since there's another function
- 01:19
in either the power of co sign a which is
- 01:22
coast on a we need to find the derivative of
- 01:24
it which is negative sign of a We multiply that
- 01:28
to what we currently have Conduce um quick simplification and
- 01:31
get rid of the limited re since that's just one
- 01:35
and we're left with either the coastline of a times
- 01:38
negative sign of a Our answer matches up with the
- 01:41
answer choice eh Hey that was not significantly less painful 00:01:45.04 --> [endTime] than taking a brick wall Approach your forehead
Up Next
AP Calculus: AB/BC Limits Drill 1, Problem 5. Evaluate the limit.
Related Videos
AP Calculus: Problem Explanation Limits Drill 1, Problem 1. Which of the following are true about the pictured function?
Breathe in deeply through the nose... Now slowly exhale... Breathe in... And out... Now visualize the graph of the limit of f(x) as x approaches 2....
AP Calculus 1.4 Limits. Given the limit, which of the following are true?
AP Calculus 2.3 Limits. Which of the following facts is helpful in determining the limit?