Distributive Property

Let's review the properties using variables instead of numbers:

	Addition	Multiplication
Commutative
Associative
Inverse
Identity

The properties above do NOT work with subtraction and division.

Distributive Property

This one is very important when working with algebraic expressions. It basically says this:

and

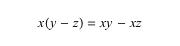
However, the distributive property does NOT work when the variables inside the parentheses are being multiplied or divided.

and

Let's go through an example very carefully:

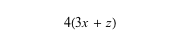
By applying the distributive property, we can multiply each term inside the parentheses by 4. This is called "distributing".

Since 12x and 4 are not like terms, this is as far as we can go with the problem.

Well, what about subtraction? Let's look at a subtraction problem using two different methods.

Method 1 Leave as Subtraction	Method 2 Add the Negative