Toddlers are funny. They're just beginning to understand the world around them, and they fall down a lot. They don't understand much, but greed is one thing they seem to get right out of the gate. As soon as they figure out how to use their opposable thumbs, they're everywhere, grabbing everything they can find.

Their favorite thing is to take things held by someone else's opposable thumbs. It doesn't make any difference what it is—toy car, aardvark plushie, brand new iPhone, pickle and onion sandwich, garbage. They don't care about whether the stuff's good or bad. They just want stuff and they take whatever stuff they can reach first.

Greedy algorithms are a little like grabby toddlers—minus the drooling and gibberish. Let's take a closer look at how they work. (And by "they," we mean greedy algorithms. Nobody knows how toddlers work.)

If you had a bunch of coins worth 1, 2, 5, 8, and 10 cents each, what's the minimum number of coins you could use to add up to 24?

Did you get 4 coins? No? Try again.

You should have

10 + 10 + 2 + 2

If you divide the target sum, 24, by the largest coin available, 10, you'll get two, with four left over. Once you have four left, you can divide it by the largest possible coin (2, for the record), to get your last two coins.

Well done. That's great work…except for the fact that it's actually wrong. Hey, you learn best from your mistakes (except when YouTube is involved). The right answer is actually three (8 + 8 + 8).

The first answer—the wrong one—used a greedy algorithm. Greedy algorithms choose the first solution they find, just like a toddler with sticky fingers (both literally and metaphorically). They aren't known for their careful diligence and weighing of the problem: they just grab the first thing and run with it. A greedy algorithm gets you to a solution, sure, but it might not be the best solution to the problem. That's fine if you just need a solution, and it doesn't need to be the optimal (best) solution.

Where they do work? Most money problems. If you give the cashier a $20 bill for your $3.35 Choco Taco, you probably don't care how you get the $16.65 in change. You might get one $10, one $5, one $1 and change. Maybe you'll get a watch, three kittens, and white fedora with small sweat stains. As long as it's all worth $16.65, who cares, right?

Except the problem we started with, of course.

You have to be careful when looking at problems, Shmooper: that money question is asking for a minimum number of coins. Whenever you're dealing with minimums or maximums, that's a problem asking for the best solution. Unlike greedy algorithms, dynamic programming cares about best solutions, which it typically calls optimized solutions. Instead of grabbing at any old solution, the dynamic programming algorithms is going to look through all the possible solutions and find the best possible option.

If you stumbled into that wrong answer, you might see that the problem's a little more complicated than it looks. The key to dynamic programming is breaking the problem down into sub-problems, so that's exactly what you have to do.

First step: create a table and plan to make three passes through it.

Pass One: Create all the possible coin combinations that add evenly to 24 using only the five possible coin values (1, 2, 5, 8, 10). There isn't a restriction on the number of coins you can use (although that might be a thing in a different problem). Just make sure it adds evenly to 24.

Pass Two: Count the number of coins it took to reach 24 for each entry and add this count to the table.

Pass Three: Make a last pass through the table and find the smallest number of coins that added to make 24

Here's the hard part: figuring out the size of the table. Since the smallest value for a coin is 1 (whether it's one cent, one rupee, one yen, or one druggat), the most coins it could totally take is 24. Any other combination of the 1, 2, 5, 8, and 10 adding to 24 would have to take fewer than 24 coins.

It's still possible to need 24 coins, though, so you'll need a maximum of 24 columns in the table to hold a coin value for each possible coin sequence that adds up to 24. You'll also want to add a column for holding the number of coins it took to reach each combination of coins. That means the size of the table needs to be 24 + 1 columns (that's 25, for the record) and n rows, where n is the total number of combinations you end up with.

There's just one, itty-bitty problem: you won't know how many coin combinations are possible until the program loads the table on Pass One. That's fine, because in bottom-up programming the entire solution isn't usually visible up front. This table will be huge, which is why you want to make the computer to load it instead of forcing yourself to spend countless hours scratching it out on paper with a pencil.

(Do you even have paper and pencils? Are they still a thing?)

The computer-generated table looks something like this:

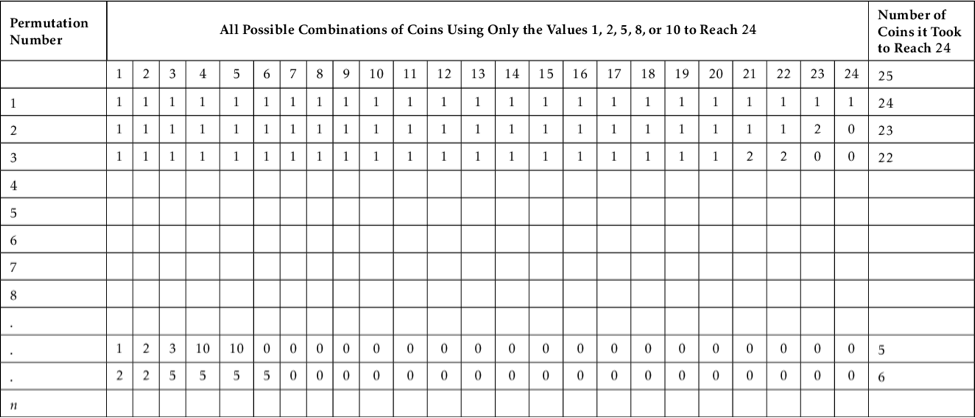
Check out some key parts to this table:

• The top row and left column tell you at which pass each value gets added. 
• Inside that row and column, every row shows a possible combination of coins. 
• The rightmost column tells you how many coins it takes to reach 24. 
• You'll load the table by recursively identifying coin combinations that add to make 24. This process is called memoization, or storing the solutions to the sub-problems in a table. (Yes, that spelling's correct. There is no r; the r is dead.)

There are some other parts to think about here:

• Each row represents a possible combination of coins adding to 24, so the sum of all the red numbers in each row must be 24. 
• The only values that can show up in each cell are 1, 2, 5, 8, or 10.
• The value in each cell in column 25 will never go over 24, because we'll never add a coin that makes us break the bank

In real life, nobody cares how many coins you use to pay for something, unless it's around a one-billion dollar payout for a patent lawsuit settlement, which Samsung did pay to Apple, but not in nickels.

(Are there even enough nickels in circulation for that?)

Coding the solution is a little more complex, but we aren't going to get into it here. If you want to see more about it, check out this video.

It involves quite a bit of math jargon. You've been warned.